Проверьте, подбирая соответствующие примеры, какие из данных форм правильные.
Выберите один или несколько ответов:
a. Если всех хищников можно приручить, а всех львов можно приручить, то все львы — хищники;
b. Если некоторых хищников можно приручить, а все львы — хищники, то некоторых львов можно приручить;
c. Если все квадраты являются прямоугольниками, то некоторые прямоугольники не являются квадратами;
d. Если ни один кит не может летать, то ни один летающий предмет не является китом;
e. Если всех львов можно приручить, а львы — хищники, то всех хищников можно приручить;
Во второй задаче вспомните, когда две прямые, заданные уравнениями, параллельны, найдите координаты точки пересечения первых двух прямых и подставьте их в уравнение искомой прямой.
В третьей задаче воспользуйтесь скалярным произведением векторов.
В четвертой задаче прежде всего запишите каноническое уравнение эллипса в общем виде.
В пятой задаче найдите уравнение прямой, координаты точки пересечения с параболой и посчитайте дину.
1. В 1 очередь надо найти область определения
Для левой части это будет x ≠ 2, ее же в этом случае приведем к виду
log√3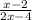
=log√3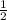
В правой части область определения x ≠ 2 и (x+1)/(x+2)>0, если x+1 >0 то и подавно x+2>0, если х+1 < 0 и x+2 <0, то x< -2, тогда x∈(-∞,-2)∪(-1,+∞), но с учетом x ≠2 имеем область определения x∈(-∞,-2)∪(-1,2)∪(2,+∞)
Теперь, избавляясь от логоарифмов
1/2= (x+1)/(x+2), x+2=2x+2
x =0
2. Тоже сначала ищем область определения
x²-9 ≥0, x ∈(-∞,-3]∪[3,+∞)
x+3 ≥ 0, x ∈ [-3,+∞)
x²+6x+9=(x+3)²≥0 ∀ x
Область определения в этом случае имеет вид x ∈ [3,+∞)
тогда имеем уравнение
x-3+2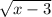
+1≥x+3
2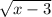
≥5
x-3 ≥ 6,25
x ≥ 9,25
3. x=2y
x-y=y, x-y+1=y+1
4y=1,
y=0,25, x=0,5
Пошаговое объяснение: