Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
dghfgjuf
14.02.2023 06:42 •
Математика
Проверьте правильность решения lim-> 0(1/x+1)^1/2x=1/lim-> 0(1+1/x)^1/x×x×1/2x=1/√е
Показать ответ
Ответ:
Даниил5356
03.10.2020 12:52
Здесь неопределенность
, следовательно, нужно применить второй замечательный предел
0,0
(0 оценок)
Популярные вопросы: Математика
kabdollaevaalia
06.12.2021 14:36
Технологическая карта изготовления оси.технологическая карта изготовления оси...
tabarovavikap06jkm
10.03.2021 08:47
Всем добрый день по задали перевести дроби сос 20 б и премяя 20 сколько сантиметров содержется в 1/10дм. 4/5дм 7/2дм. и 6/5 если вы объяснить как это решать тогда (если...
вероника1060
16.06.2021 18:23
46+(-46)= -93+7= (+15+)(+15)= (-9)+58= 0+(-18)= 81+(-19)= -12+(-64) +5+0= (+36)+(-36)= 21+(-59)= (-94)+(+6)= -12+12= прощу вас )...
lanakalina
01.01.2022 17:36
Квадраттын кабыргасы4см ден артык .5см ден кем .квадратын перимедрын багаландар отыныш комектесындершы...
anastasiyapauk
22.08.2021 05:11
Решите : при каком б уравнения будут равносильны: 2x-9=3 и x+3b=-10...
Kseniyak04
03.12.2021 04:00
Написать сочинение по любому одному стиху хади такташа (на )...
Варя11011
03.12.2021 04:00
На метод зрівнювання на трьох верстатах виготовили 414 деталей. на першому верстаті виготовили на 8 деталей менше, ніж на другому,а на другому верстаті на 10 деталей...
саша3347
25.06.2021 05:30
Угол д данного треугольника в три раза больше угла ц но на половину меньше угла л .определите величины углов треугольника...
qwerty91a
25.06.2021 05:30
Каа решить уравнение (18: 9): х=324: 4 х: (290-140)=48: 8...
ALEXGEEK
25.06.2021 05:30
Сколько в домино костей с десяткой ?...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Здесь неопределенность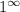 , следовательно, нужно применить второй замечательный предел
, следовательно, нужно применить второй замечательный предел