Пусть даны n типов заготовок с номерами 1,...,n и длинами , а исходные стержни имеют длину .
В начале поиска полагаем i=1
1. Ищем максимально возможное число заготовок типа i. Оно, очевидно, равно , где [х] - целая часть числа x.
2. Ищем длину незадействованной части стержня. Она, очевидно, равна
3. Если существует заготовка с номером, большим i, и длиной, меньшей S', и решаем аналогичную задачу для стержня длиной S' и заготовок с номерами i+1,...,n. Иначе пункт 4.
4. Получен вариант раскроя. Записываем число отходов.
5. Если N≥1 и i≠n, уменьшаем N на 1, и решаем аналогичную задачу для стержня длиной и заготовок с номерами i+1,...,n
Пошаговое объяснение: в приложении
Построение раскроев
Пусть даны n типов заготовок с номерами 1,...,n и длинами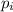 , а исходные стержни имеют длину
, а исходные стержни имеют длину 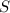 .
.
В начале поиска полагаем i=1
1. Ищем максимально возможное число заготовок типа i. Оно, очевидно, равно![N=\left[\dfrac{S}{p_i}\right]](/tpl/images/1537/7845/f1eeb.png) , где [х] - целая часть числа x.
, где [х] - целая часть числа x.
2. Ищем длину незадействованной части стержня. Она, очевидно, равна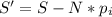
3. Если существует заготовка с номером, большим i, и длиной, меньшей S', и решаем аналогичную задачу для стержня длиной S' и заготовок с номерами i+1,...,n. Иначе пункт 4.
4. Получен вариант раскроя. Записываем число отходов.
5. Если N≥1 и i≠n, уменьшаем N на 1, и решаем аналогичную задачу для стержня длиной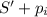 и заготовок с номерами i+1,...,n
и заготовок с номерами i+1,...,n
Пошаговое объяснение:
V=(a*b)*h
h= V:(a*b)
так как известны длина и ширина, то можно найти из обьема высоту:
1) h=60:(6*5)=2 (дм)
Имея длину, ширину, высоту, можно найти площадь прямоугольного
параллелепипеда:
S = 2 * ( a*b+b*h+a*h)
2) S = 2* ( 6*5+5*2+6*2)=104 дм²
ответ: площадь прямоугольного параллелепипеда равна 104 дм².
Покрокове пояснення:
V = (a * b) * h
h = V: (a * b)
так як відомі довжина і ширина, то можна знайти з обьема висоту:
1) h = 60: (6 * 5) = 2 (дм)
Маючи довжину, ширину, висоту, можна знайти площу прямокутного
паралелепіпеда:
S = 2 * (a * b + b * h + a * h)
2) S = 2 * (6 * 5 + 5 * 2 + 6 * 2) = 104 дм²
Відповідь: площа прямокутного паралелепіпеда дорівнює 104 дм².