1. Если числа n и m - четные, то n = 2p, m = 2q, где p и q - целые числа. Тогда n + m = 2p + 2q = 2(p + q) - очевидно, четное число, что и требовалось доказать.
2. Предположим, что n - нечетное, и его квадрат равен четному числу. n = 2p + 1, где p - целое число. Тогда n² = (2p + 1)² = (2p)² + 2 · 2p · 1 + 1² = 4p² + 4p + 1 = 4p(p + 1) + 1 - очевидно, нечетное число при любом целом p. Получили противоречие - следовательно, n - четное.
3. Предположим, что если (n + m) - нечетное число, то возможно, что оба слагаемых являются или числами четными, или числами нечетными.
Если n и m - четные, то n = 2p, m = 2q. Тогда n + m = 2p + 2q = 2(p+q) - четное число, а не нечетное. Получили противоречие - следовательно, числа n и m не могут одновременно быть четными.
Если n и m - нечетные числа, то n = 2p + 1, m = 2q + 1. Тогда n + m = (2p + 1) + (2q + 1) = 2p + 2q + 2 = 2(p + q + 1) - четное, а не нечетное число. Получили противоречие - следовательно, n и m не могут быть нечетными одновременно.
Следовательно, одно из чисел четное, другое - нечетное, что и требовалось доказать.
1) когда всего 17 изделий и 7 некачественных, находим вероятность, при которой нам попадается брак.
2) после этого получается следующее: 17 - 1 = 16, 7 - 1 = 6, так как 1 деталь мы уже забрали то есть нам нужно вычесть со всех изделий эту деталь и соответственно с некачественных тоже, так как они напрямую зависят друг от друга.
3) по теореме произведения зависимых событий, где нужно 2 события перемножить, из которых одно предполагаемое (первое событие), а второе условное идёт за ним в дальнейшем. Формула P (AB) = P (A) x P (B), где A и B - события .
1. Если числа n и m - четные, то n = 2p, m = 2q, где p и q - целые числа. Тогда n + m = 2p + 2q = 2(p + q) - очевидно, четное число, что и требовалось доказать.
2. Предположим, что n - нечетное, и его квадрат равен четному числу. n = 2p + 1, где p - целое число. Тогда n² = (2p + 1)² = (2p)² + 2 · 2p · 1 + 1² = 4p² + 4p + 1 = 4p(p + 1) + 1 - очевидно, нечетное число при любом целом p. Получили противоречие - следовательно, n - четное.
3. Предположим, что если (n + m) - нечетное число, то возможно, что оба слагаемых являются или числами четными, или числами нечетными.
Если n и m - четные, то n = 2p, m = 2q. Тогда n + m = 2p + 2q = 2(p+q) - четное число, а не нечетное. Получили противоречие - следовательно, числа n и m не могут одновременно быть четными.
Если n и m - нечетные числа, то n = 2p + 1, m = 2q + 1. Тогда n + m = (2p + 1) + (2q + 1) = 2p + 2q + 2 = 2(p + q + 1) - четное, а не нечетное число. Получили противоречие - следовательно, n и m не могут быть нечетными одновременно.
Следовательно, одно из чисел четное, другое - нечетное, что и требовалось доказать.
1)
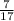-при выборе первого изделия (первое событие)
2)
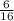- при выборе второго изделия (второе событие)
3)
×
= 
= 
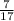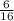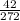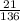
ответ. Вероятность равна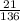
Пошаговое объяснение:
1) когда всего 17 изделий и 7 некачественных, находим вероятность, при которой нам попадается брак.
2) после этого получается следующее: 17 - 1 = 16, 7 - 1 = 6, так как 1 деталь мы уже забрали то есть нам нужно вычесть со всех изделий эту деталь и соответственно с некачественных тоже, так как они напрямую зависят друг от друга.
3) по теореме произведения зависимых событий, где нужно 2 события перемножить, из которых одно предполагаемое (первое событие), а второе условное идёт за ним в дальнейшем. Формула P (AB) = P (A) x P (B), где A и B - события .