Прямоугольник состоит из клеток со стороной 1. Некоторые из клеток закраше
ны. Оказалось, что закрашенных клеток в каждой строке ровно 5, а в каждом
столбце - ровно 6. Чему может быть равна площадь такого прямоугольника?

(А) 96 (Б) 100 (В) 108
(0) 115 (Д) 120

Показать ответ

Ответ:

Про100Володя

11.10.2020 22:47

Рассмотрим наименьший такой прямоугольник. Это прямоугольник из 6 строк и 5 столбцов, в котором все клетки закрашены. Площадь его равна 30.

Если мы захотим добавить еще одну строку, то в ней также надо будет закрасить 5 клеток, но тогда во всех столбцах уже окажется закрашенными более 6 клеток. Значит, нам придется добавить еще 5 столбцов, в каждом из которых мы будем закрашивать клетки этой строки. Мало того, нам придется добавить еще 5 строк, чтобы выполнить условие о том, что во всех столбцах ровно 6 закрашенных клеток, а значит докрасить клетки, соответствующие столбцам из ранее добавленной строки. В результате число строк и число столбцов удвоилось, а площадь увеличилась в 4 раза и стала равной 120. Закрашенные клетки впоследствии можно менять местами, придерживаясь ограничений на них, но от этого размеры прямоугольника не изменятся.

Аналогично, исходная площадь 30 может увеличиться в 9, 16, 25 и так далее раз.

В общем виде возможная площадь выражается формулой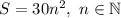 $S=30n^2, \ n\in\mathbb{N}$ . Из вариантов ответов подходит лишь число 120, которое как раз и получилось при рассуждениях.