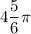ABCDA1B1D1C1 - фигура, образованная двумя горизонтально расположенными квадратами ABCD и A1B1D1C1 и четырьма вертикальными АА1В1СД, ВВ1С1С, СС1Д1Д и ДД1А1А.
Как видим, прямые B1D1 и DC1 являются диагоналями соответственно горизонтального и вертикального квадратов, не лежат в одной плоскости и являются скрещивающимися.
Для решения нашей задачи нужно провести прямую BD, параллельную B1D1. Угол между BD и DC1 равен искомому углу.
Построим BD и соединим точки B, Dи С1.
Получили ΔBDС1, где BD = DC1 = ВС1, т.к. все три стороны есть диагонали равных квадратов - граней куба ABCDA1B1D1C1.
А в равностороннем треугольнике все внутренние углы равны по 60°.
60°
Пошаговое объяснение:
ABCDA1B1D1C1 - фигура, образованная двумя горизонтально расположенными квадратами ABCD и A1B1D1C1 и четырьма вертикальными АА1В1СД, ВВ1С1С, СС1Д1Д и ДД1А1А.
Как видим, прямые B1D1 и DC1 являются диагоналями соответственно горизонтального и вертикального квадратов, не лежат в одной плоскости и являются скрещивающимися.
Для решения нашей задачи нужно провести прямую BD, параллельную B1D1. Угол между BD и DC1 равен искомому углу.
Построим BD и соединим точки B, Dи С1.
Получили ΔBDС1, где BD = DC1 = ВС1, т.к. все три стороны есть диагонали равных квадратов - граней куба ABCDA1B1D1C1.
А в равностороннем треугольнике все внутренние углы равны по 60°.
I. (2sin²x - 7sinx + 3) · log₂ (x-8) = 0
ОДЗ : x-8 > 0; x > 8
Произведение равно нулю, когда один из множителей равен нулю.
1) 2sin²x - 7sinx + 3 = 0 - квадратное уравнение с неизвестным sinx
D = 7² - 4·2·3 = 25 = 5²
sin x = (7+5)/4 = 3 - не подходит под условие |sin x| ≤ 1
sin x = (7-5)/4 = 1/2
x₁ = π/6 + 2πn, n∈N, n≥2 ( ОДЗ: π/6 + 4π ≈ 13,1 > 8)
x₂ = 5π/6 + 2πk, k∈N ( ОДЗ: 5π/6 + 2π ≈ 8,9 > 8)
2) log₂ (x-8) = 0 ⇒ x - 8 = 2⁰
x = 1 + 8; x₃ = 9
==========================
II. x ∈ (3π; 6π)
3) x₃ = 9 < 9,4 ≈ 3π - не входит в интервал
ответ: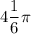 ;
;