Пошаговое объяснение:
Неизвестную величину обозначим через Х, тогда
чтобы найти 20% от нее, надо х·0,20=0,2х
чтобы увеличить ее, например, на 10%, надо х+0,10·х=1,1х
чтобы уменьшить ее, например, на 30%, надо х+0,30·х=1,3х
Увеличьте 60р. на 20% 60+60·0,20= 60+12=72
Увеличьте 80р. на 40% 80+ 80·0,40= 80+32=112
Уменьшить 300р. на 30% 300 - 300·0,30= 300 - 90=210
Что значит найти 10 %, 20 % от величины? Найти 10 % или 20 % от величины значит умножить эту величину на 0,10 или на 0,20.
Найти 70% от 18 18·0,70= 12,6
Если для любого из области определения функции выполняется равенство , то функция является чётной.
Если для любого из области определения функции выполняется равенство , то данная функция является нечётной.
Если же ни одно из этих равенств не выполняется, то функция не является ни чётной, ни нечётной.
б)
Отсюда .
Для начала найдём область определения данной функции. Её знаменатель не должен быть равен нулю:
Итак, область определения нашли. Теперь найдём , для этого все в функции заменим на .
Таким образом, данная функция является нечётной.
в)
То есть, для данной функции за можно принять любое действительное число. Теперь найдём , для этого все в функции заменим на .
Таким образом, данная функция является чётной.
г)
может быть любым числом, поскольку никаких ограничений на аргумент здесь не накладывается. Теперь найдём , для этого все в функции заменим на .
.
и , а значит, функция не является ни чётной, ни нечётной.
Пошаговое объяснение:
Неизвестную величину обозначим через Х, тогда
чтобы найти 20% от нее, надо х·0,20=0,2х
чтобы увеличить ее, например, на 10%, надо х+0,10·х=1,1х
чтобы уменьшить ее, например, на 30%, надо х+0,30·х=1,3х
Увеличьте 60р. на 20% 60+60·0,20= 60+12=72
Увеличьте 80р. на 40% 80+ 80·0,40= 80+32=112
Уменьшить 300р. на 30% 300 - 300·0,30= 300 - 90=210
Что значит найти 10 %, 20 % от величины? Найти 10 % или 20 % от величины значит умножить эту величину на 0,10 или на 0,20.
Найти 70% от 18 18·0,70= 12,6
Если для любого из области определения функции выполняется равенство
из области определения функции выполняется равенство 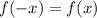 , то функция является чётной.
, то функция является чётной.
Если для любого из области определения функции выполняется равенство
из области определения функции выполняется равенство 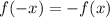 , то данная функция является нечётной.
, то данная функция является нечётной.
Если же ни одно из этих равенств не выполняется, то функция не является ни чётной, ни нечётной.
б)
Отсюда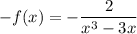 .
.
Для начала найдём область определения данной функции. Её знаменатель не должен быть равен нулю:
Итак, область определения нашли. Теперь найдём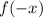 , для этого все
, для этого все  в функции заменим на
в функции заменим на 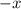 .
.
Таким образом, данная функция является нечётной.
в)
Отсюда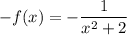 .
.
Для начала найдём область определения данной функции. Её знаменатель не должен быть равен нулю:
То есть, для данной функции за можно принять любое действительное число. Теперь найдём
можно принять любое действительное число. Теперь найдём 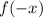 , для этого все
, для этого все  в функции заменим на
в функции заменим на 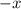 .
.
Таким образом, данная функция является чётной.
г)
Отсюда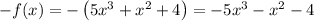 .
.