РАБОТА В ГРУППЕ Выполни задание. иши, какая часть окружности закра- а Какая часть не закрашена? Проведи еобходимые измерения и начерти в тет- ради окружность такого же размера,
Пусть скорость первого бегуна км/ч. Тогда скорость второго равна км/ч. Попробуем по-разному выразить длину круга. Обращаю внимание, что мы будем все выражать в км, ч и км/ч.
С одной стороны, это , так как первый бегун бежал минут ( ч) со скоростью и ему еще осталось метров ( км)
С другой стороны, весь круг - это просто , так как второй спортсмен пробежал весь круг за минут или часа.
Составим и решим уравнение!
Таким образом, скорость первого бегуна - км/ч. Задача решена!
Пифагор вывел соотношение длин катетов и длины гипотенузы в ПРЯМОУГОЛЬНОМ треугольнике.
Возьмем квадрат со стороной С. Поместим этом квадрат в другой квадрат побольше, но так, чтобы вершины квадрата со стороной С касались с сторон большего квадрата так, чтобы каждая сторона большего квадрата делилась на отрезки длиной А и В.
Мы получим следующий рисунок: Большой квадрат со стороной А+В состоит из меньшего квадрата со стороной С и четырех маленьких треугольников, в каждом из которых катеты равны А и В, а гипотенуза равна С.
Пусть скорость первого бегуна км/ч. Тогда скорость второго равна
км/ч. Тогда скорость второго равна 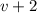 км/ч. Попробуем по-разному выразить длину круга. Обращаю внимание, что мы будем все выражать в км, ч и км/ч.
км/ч. Попробуем по-разному выразить длину круга. Обращаю внимание, что мы будем все выражать в км, ч и км/ч.
С одной стороны, это , так как первый бегун бежал
, так как первый бегун бежал 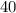 минут (
минут (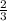 ч) со скоростью
ч) со скоростью 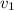 и ему еще осталось
и ему еще осталось 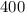 метров (
метров (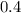 км)
км)
С другой стороны, весь круг - это просто , так как второй спортсмен пробежал весь круг за
, так как второй спортсмен пробежал весь круг за 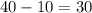 минут или
минут или 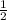 часа.
часа.
Составим и решим уравнение!
Таким образом, скорость первого бегуна -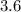 км/ч. Задача решена!
км/ч. Задача решена!
ответ: 3.6 км/ч.Возьмем квадрат со стороной С.
Поместим этом квадрат в другой квадрат побольше, но так, чтобы вершины квадрата со стороной С касались с сторон большего квадрата так, чтобы каждая сторона большего квадрата делилась на отрезки длиной А и В.
Мы получим следующий рисунок:
Большой квадрат со стороной А+В состоит из меньшего квадрата со стороной С и четырех маленьких треугольников, в каждом из которых катеты равны А и В, а гипотенуза равна С.
Площадь каждого треугольника равна
А•В/2
Площадь маленького квадрата равна
С²
Площадь большого квадрата равна
(А+В)²
Запишем равенство:
(А+В)² = С² + 4 • А•В/2
(А+В)•(А+В) = С² + 2А•В
А² + А•В + А•В + В² = С² + 2А•В
А² + 2А•В + В² = С² + 2А•В
А² + 2А•В + В² - 2А•В = С²
А² + В² = С²
Таким образом, мы получили соотношение длин сторон в прямоугольном треугольнике:
СУММА КВАДРАТОВ КАТЕТОВ РАВНА КВАДРАТУ ГИПОТЕНУЗЫ
или
А² + В² = С²
где А и В - катеты, а С - гипотенуза.