2) Общего у них механизм действия: ножовка имеет зубья клиновидной формы так и напильник имеет сформированную поверхность которая тоже образовывает зубья клиновидной формы.
3)поперечным штрихом,продольным штрихом,закреплённая в вертикальном положении,закреплённая в горизонтальном положении,малого радиуса и большого радиуса
4) Особенность рашпиля в том, что он имеет насечку в виде отдельно расположенных выступов или зубьев.
5) многолезвийный инструмент для обработки металлов, дерева, пластмасс и других твёрдых материалов.
6) Бархатные напильники служат для точных опиловочных работ при снятии слоя 0 1 мм, с точностью 0 005 - 0 02 мм.. Бархатные напильники применяют для самой точной обработки и придания обрабатываемой поверхности высокой чистоты. Для доводочных и других специальных работ применяют напильники, называемые надфилями. Они имеют самую мелкую насечку.
Пошаговое объяснение:
1) плоские, квадратные, полукруглые,трехгранные,круглые,ножовочные,ромбические
2) Общего у них механизм действия: ножовка имеет зубья клиновидной формы так и напильник имеет сформированную поверхность которая тоже образовывает зубья клиновидной формы.
3)поперечным штрихом,продольным штрихом,закреплённая в вертикальном положении,закреплённая в горизонтальном положении,малого радиуса и большого радиуса
4) Особенность рашпиля в том, что он имеет насечку в виде отдельно расположенных выступов или зубьев.
5) многолезвийный инструмент для обработки металлов, дерева, пластмасс и других твёрдых материалов.
6) Бархатные напильники служат для точных опиловочных работ при снятии слоя 0 1 мм, с точностью 0 005 - 0 02 мм.. Бархатные напильники применяют для самой точной обработки и придания обрабатываемой поверхности высокой чистоты. Для доводочных и других специальных работ применяют напильники, называемые надфилями. Они имеют самую мелкую насечку.
1. Метод исключения неизвестных.
Продифференцируем первое уравнение:
Подставим выражение для y':
Из получившегося уравнения отнимем первое уравнение системы:
Составим характеристическое уравнение:
Найдем производную:
Выразим из первого уравнение системы у:
Общее решение:
Находим решение задачи Коши:
Первое уравнение домножим на 2:
Сложим уравнения:
Выразим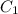
:
Частное решение:
2. Метод характеристических уравнений (метод Эйлера).
Матрица из коэффициентов при неизвестных:
Характеристическая матрица:
Характеристическое уравнение:
Общее решение:
Ищем фундаментальную систему решений:
Для нахождения чисел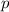
составим систему:
Для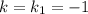
:
Оба уравнения дают:
Найдем ненулевое решение. Пусть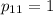
. Тогда 
.
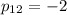Для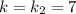
:
Оба уравнения дают:
Найдем ненулевое решение. Пусть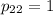
. Тогда 
.
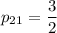Фундаментальная система решений найдена:
Общее решение:
Находим частное решение:
Первое уравнение домножим на 2:
Сложим уравнения:
Выразим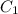
:
Частное решение: