ответ: (7/9); 0.875; (15/16); (16/17).
Объяснение:
есть такой прием - сравнение двух дробей с 1 или с (1/2)...
в общем случае, чтобы сравнить две обыкновенные дроби, нужно привести их к общему знаменателю...
если знаменатели одинаковые, то дробь тем больше, чем больше числитель...
если числители одинаковые, то дробь тем больше, чем меньше знаменатель (обратная зависимость)...
...очень не хочется искать НОК(16;17) -это общий знаменатель...
на числовой прямой от числа (15/16) до 1 расстояние = (1/16);
от числа (16/17) до 1 расстояние = (1/17)... ,
т.е. 15/16 ближе к 0, а значит меньше...
7 / 9 = (7*16) / (9*16) = 112 / 144
15 / 16 = (15*9) / (16*9) = 135 / 144 > 7/9
0.875 = 875 / 1000 = 35 / 40 = 7 / 8 > 7 / 9
0.875 = 7 / 8 = 14 / 16 < 15 / 16
Пошаговое объяснение:
7/9=0.77(7)
15/16=0.9375
16/17=0.941
7/9; 0.875: 15/16; 16/17
ответ: (7/9); 0.875; (15/16); (16/17).
Объяснение:
есть такой прием - сравнение двух дробей с 1 или с (1/2)...
в общем случае, чтобы сравнить две обыкновенные дроби, нужно привести их к общему знаменателю...
если знаменатели одинаковые, то дробь тем больше, чем больше числитель...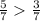
если числители одинаковые, то дробь тем больше, чем меньше знаменатель (обратная зависимость)...
...очень не хочется искать НОК(16;17) -это общий знаменатель...
на числовой прямой от числа (15/16) до 1 расстояние = (1/16);
от числа (16/17) до 1 расстояние = (1/17)... ,
,
т.е. 15/16 ближе к 0, а значит меньше...
7 / 9 = (7*16) / (9*16) = 112 / 144
15 / 16 = (15*9) / (16*9) = 135 / 144 > 7/9
0.875 = 875 / 1000 = 35 / 40 = 7 / 8 > 7 / 9
0.875 = 7 / 8 = 14 / 16 < 15 / 16
Пошаговое объяснение:
7/9=0.77(7)
15/16=0.9375
16/17=0.941
7/9; 0.875: 15/16; 16/17