Предположим противное, то есть то, что Вася всегда сможет выписать очередное число. В силу попарного различия выписываемых чисел, их множество неограниченно.
Рассмотрим первые 9 чисел. Пусть у них есть общий делитель . Заменим теперь последнее число (9-ое в последовательности) на 10-ое в последовательности. Чисел снова 9 и у них должен быть общий делитель . Если при этом , то можно взять первые 10 чисел и у них окажется общий делитель , противоречие. Значит, и взаимно просты. Далее заменяем 10-ое число на 11-ое и так далее. Получаем бесконечное множество чисел, поскольку они попарно взаимно просты. Но все эти числа делят первые 8 чисел множества, у которых множество делителей, очевидно, ограничено. Противоречие. Следовательно, в какой-то момент Вася не сможет выписать очередное число.
20 - дневная производительность труда мастера до начала соревнования;
24 - дневная производительность труда мастера в ходе соревнования;
10 - дневная производительность ученика до начала соревнования;
11 - дневная производительность ученика в ходе соревнования.
Пошаговое объяснение:
Пусть первоначальная дневная производительность труда мастера равна х, а первоначальная дневная производительность одного ученика равна у.
Тогда можно составить следующую систему уравнений:
(5х + 7у) · 5 = 850 (1)
(5х · 1,2 + 7у · 1,1) · 5 = 985 (2)
или
5х + 7у = 170 (3)
6х + 7,7 у = 197 (4)
Умножим уравнение (3) на 1,1:
5,5 х + 7,7 у = 187 (5)
и из уравнение (4) вычтем уравнение (5):
6х - 5,5х + 7,7у - 7,7у = 197 - 187
0,5х = 10
х = 20 - дневная производительность труда мастера до начала соревнования;
20 · 1,2 = 24 - дневная производительность труда мастера в ходе соревнования.
Подставим х = 20 в уравнение (3):
5 · 20 + 7у = 170
7у = 170 - 100 = 70
у = 70/7 = 10 - дневная производительность ученика до начала соревнования;
10· 1,1 = 11 - дневная производительность ученика в ходе соревнования.
ПРОВЕРКА
(5 · 20 + 7 · 10) · 5 = 850
(5 · 24 + 7 · 11) · 5 = 985
20 - дневная производительность труда мастера до начала соревнования;
24 - дневная производительность труда мастера в ходе соревнования;
10 - дневная производительность ученика до начала соревнования;
11 - дневная производительность ученика в ходе соревнования.
Предположим противное, то есть то, что Вася всегда сможет выписать очередное число. В силу попарного различия выписываемых чисел, их множество неограниченно.
Рассмотрим первые 9 чисел. Пусть у них есть общий делитель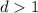
. Заменим теперь последнее число (9-ое в последовательности) на 10-ое в последовательности. Чисел снова 9 и у них должен быть общий делитель 
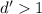. Если при этом 
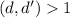, то можно взять первые 10 чисел и у них окажется общий делитель 
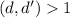, противоречие. Значит, 
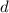и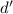 
взаимно просты. Далее заменяем 10-ое число на 11-ое и так далее. Получаем бесконечное множество чисел, поскольку они попарно взаимно просты. Но все эти числа делят первые 8 чисел множества, у которых множество делителей, очевидно, ограничено. Противоречие. Следовательно, в какой-то момент Вася не сможет выписать очередное число.