По определению логарифма заметим, что основание (a) всегда должно быть больше "0" и не равное "1". Число "b" всегда строго положительное, т.к. при возведение любого положительного числа "а" в любую степень "с", мы получим строго положительное значение.
Рассмотрим наше уравнение:
ОДЗ (область допустимых значений):
Используем потенцирования, т.е. отбросим часть с логарифмом (мы имеем на это право, т.к. основание у логарифмов одинаковые и никаких посторонних членов нет)
По определению логарифма заметим, что основание (a) всегда должно быть больше "0" и не равное "1". Число "b" всегда строго положительное, т.к. при возведение любого положительного числа "а" в любую степень "с", мы получим строго положительное значение.
Рассмотрим наше уравнение:
Используем потенцирования, т.е. отбросим часть с логарифмом (мы имеем на это право, т.к. основание у логарифмов одинаковые и никаких посторонних членов нет)
Запишем ответ:
ответ: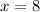
lg^2 (10x) + lg(10x) = 6 - 3lg(1/x)
lg^2 (10x) + lg(10x) = 6 + 3lg(x)
lg^2 (10x) + lg(10x) = 6 + (3lg(x) + 3lg10) -3lg10
lg^2 (10x) + lg(10x) = 6 + 3lg(10x) - 3lg10
lg^2 (10x) + lg(10x) - 3lg(10x) = 6 -3
lg^2 (10x) - 2lg(10x) -3 =0
Замена переменных
lg(10x) = y
y^2 - 2y - 3 = 0
D = 4+12 =16
y1= (2 - 4)/2 = -1; y2 = (2 + 4)/2 = 3
Находим х
при y1=-1
lg(10x) = -1
10x = 0,1
x1= 0,01
при y2 = 3
lg(10x) = 3
10x = 1000
x2 = 100
ответ: 0,01;100