Расстояние от города до центра 340 км.чтобы попасть из города в центр .студент ехал 3 часа на автобусе со скоростью 75 км/ч.оставшийся путь он проехал на машине .какое расстояние проехал студент на машине надо.соч идет.нужно с уравнения
так как лежат на одной плоскости (которая проходит через прямые и ) которая образует параллельные прямые и пересекаясь с параллельными плоскостями.
Из свойства накрест лежащих углов полученные при пересечении секущей имеем что углы ∠ и ∠ равны. Так же равны накрест лежащие углы ∠ и ∠.
Из подобия треугольников Δ и Δ следует пропорциональность сторон . Обозначим , тогда и . Подставив в пропорцию и учитывая последнее в пропорцию выше имеем следующее уравнение:
, то есть это круг (с границей), с центром в точке и радиусом . Среди точек этого множества требуется найти такие, для которых принимает наибольшее значение. Понятно также, что никакая точка внутренности не является искомой, поскольку ее можно сдвинуть на вектор для некоторого . Потому точки ищем на границе.
Рассмотрим прямую . Требуется максимизировать , то есть увеличивать это значение до тех пор, пока эта прямая имеет пересечения с окружностью. Предельный случай -- касание. Имеем: , , откуда . Тогда и .
Пошаговое объяснение:
Δ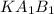 и Δ
и Δ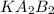 подобны по второму признаку:
подобны по второму признаку:
Из свойства накрест лежащих углов полученные при пересечении секущей имеем что углы ∠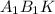 и ∠
и ∠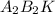 равны. Так же равны накрест лежащие углы ∠
равны. Так же равны накрест лежащие углы ∠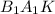 и ∠
и ∠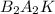 .
.
Из подобия треугольников Δ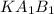 и Δ
и Δ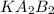 следует пропорциональность сторон
следует пропорциональность сторон 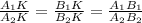 . Обозначим
. Обозначим 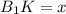 , тогда
, тогда 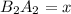 и
и  . Подставив в пропорцию
. Подставив в пропорцию  и учитывая последнее в пропорцию выше имеем следующее уравнение:
и учитывая последнее в пропорцию выше имеем следующее уравнение:
откуда имеем, что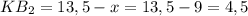 .
.
Рассмотрим прямую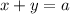 . Требуется максимизировать
. Требуется максимизировать  , то есть увеличивать это значение до тех пор, пока эта прямая имеет пересечения с окружностью. Предельный случай -- касание. Имеем:
, то есть увеличивать это значение до тех пор, пока эта прямая имеет пересечения с окружностью. Предельный случай -- касание. Имеем:  ,
,  , откуда
, откуда 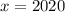 . Тогда
. Тогда 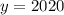 и
и  .
.