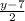\begin{gathered}\int\limits \frac{dx}{ \sqrt[5]{ {x}^{2} } } = \int\limits {x}^{ - \frac{2}{5} } dx = \frac{ {x}^{ \frac{3}{5} } }{ \frac{3}{5} } + C= \frac{5 \sqrt[5]{ {x}^{3} } }{3} + C\\ \end{gathered}∫5x2dx=∫x−52dx=53x53+C=355x3+C
2
\begin{gathered}\int\limits \frac{dx}{ \sin {}^{2} (1 - 2x) } = - \frac{1}{2} \int\limits \frac{d(1 - 2x)}{ \sin {}^{2} (1 - 2x) } = \\ = \frac{1}{2} ctg(1 - 2x) + C\end{gathered}∫sin2(1−2x)dx=−21∫sin2(1−2x)d(1−2x)==21ctg(1−2x)+C
Пошаговое объяснение:
тслслслсллслмллм
1) х=3y-5
2) x=
1) x−3y+5=0
Прибавьте 3y к обеим частям. Если прибавить к любому числу ноль, то это число не изменится.
x+5 = 3y
Вычтите 5 из обеих частей уравнения.
x = 3y−5
2) −2x+y−7 = 0
Вычтите y из обеих частей уравнения. Если вычесть любое число из нуля, то получится его отрицательный эквивалент.
−2x−7 = −y
Прибавьте 7 к обеим частям.
−2x = −y+7
Уравнение имеет стандартный вид.
−2x = 7−y
Разделите обе части на −2.
=
Деление на −2 аннулирует операцию умножения на −2.
x =
Разделите −y+7 на −2.
\begin{gathered}\int\limits \frac{dx}{ \sqrt[5]{ {x}^{2} } } = \int\limits {x}^{ - \frac{2}{5} } dx = \frac{ {x}^{ \frac{3}{5} } }{ \frac{3}{5} } + C= \frac{5 \sqrt[5]{ {x}^{3} } }{3} + C\\ \end{gathered}∫5x2dx=∫x−52dx=53x53+C=355x3+C
2
\begin{gathered}\int\limits \frac{dx}{ \sin {}^{2} (1 - 2x) } = - \frac{1}{2} \int\limits \frac{d(1 - 2x)}{ \sin {}^{2} (1 - 2x) } = \\ = \frac{1}{2} ctg(1 - 2x) + C\end{gathered}∫sin2(1−2x)dx=−21∫sin2(1−2x)d(1−2x)==21ctg(1−2x)+C
Пошаговое объяснение:
тслслслсллслмллм
1) х=3y-5
2) x=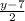
Пошаговое объяснение:
1) x−3y+5=0
Прибавьте 3y к обеим частям. Если прибавить к любому числу ноль, то это число не изменится.
x+5 = 3y
Вычтите 5 из обеих частей уравнения.
x = 3y−5
2) −2x+y−7 = 0
Вычтите y из обеих частей уравнения. Если вычесть любое число из нуля, то получится его отрицательный эквивалент.
−2x−7 = −y
Прибавьте 7 к обеим частям.
−2x = −y+7
Уравнение имеет стандартный вид.
−2x = 7−y
Разделите обе части на −2.
Деление на −2 аннулирует операцию умножения на −2.
x =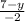
Разделите −y+7 на −2.
x =