Область определения функции — это множество всех значений, которые может принимать переменная .
может быть как , так , тут ограничений нет.
А вот подкоренное выражение может быть только , так как квадратный корень из отрицательного числа найти нельзя. Составим неравенство:
Тут два варианта - либо оба выражения ( и ) , тогда минус на минус даст плюс и конечное выражение будет , либо оба выражения . На оба случая составим системы уравнений и решим их:
1.
можно сократить до просто
2.
можно сократить до
Также (или ) т.к. на ноль делить нельзя, но мы никаких корректировок не вносим потому что у нас и так в обоих случаях )
На нашем луче от нуля до единицы вмещается 6 см. Это нам дано по условию задачи. Вот, на моих рисунках каждая черточка на прямой — это 1 см, от нуля до единицы их шесть.
Что такое 1/6? Это одна часть от шести частей. То есть, 1 см от 6 см. <рисунок1>
Луч длиной 1 см.
Что такое 1/3? Это одна часть от трёх частей.
Делим 6 см на три части, получается три части по 2 см. Чертим луч в 2 см, это 1/3. <рисунок2>
Что такое 1/2? Одна часть от двух частей, половина. Половина от шести будет три. Луч будет в 3 см. <рисунок3>
Что такое 3/6? Это три части от шести, три раза по 1/6 три раза по 1 см; 3/6 — это же и половина, это же 1/2, это же луч длиной в 3 см. <рисунок3>
Так, по аналогии, и с другими дробями:
1/6 — это луч длиной 1 см,
3/6 — это луч длиной 3 см,
5/6 — это луч длиной 5 см,
2/6 — это луч длиной 2 см,
1/3 — это луч длиной 2 см,
2/3 — это луч длиной 4 см,
1/2 — это луч длиной 3 см.
Проще говоря, можно умножить 6 (6 см, единичный отрезок, данный по условию задачи) на дробь и получить число (в см) , равное длине луча.
Например,
.
Некоторые лучи совпадают, это 3/6 и 1/2; 2/6 и 1/3. Потому что эти дроби равны. 3/6, если сократить, получится 1/2. 2/6 тоже сокращается до 1/3.
D(f) = (−∞, 2) или (2, +∞)
Пошаговое объяснение:
Область определения функции — это множество всех значений, которые может принимать переменная .
.
А вот подкоренное выражение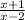 может быть только
может быть только 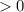 , так как квадратный корень из отрицательного числа найти нельзя. Составим неравенство:
, так как квадратный корень из отрицательного числа найти нельзя. Составим неравенство:
Тут два варианта - либо оба выражения (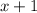 и
и 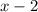 )
)  , тогда минус на минус даст плюс и конечное выражение
, тогда минус на минус даст плюс и конечное выражение 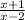 будет
будет 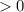 , либо оба выражения
, либо оба выражения 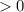 . На оба случая составим системы уравнений и решим их:
. На оба случая составим системы уравнений и решим их:
1.
2.
Также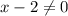 (или
(или 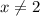 ) т.к. на ноль делить нельзя, но мы никаких корректировок не вносим потому что у нас и так в обоих случаях
) т.к. на ноль делить нельзя, но мы никаких корректировок не вносим потому что у нас и так в обоих случаях 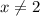 )
)
И так, конечный ответ:
D(f) = (−∞, 2) или (2, +∞)
На нашем луче от нуля до единицы вмещается 6 см. Это нам дано по условию задачи. Вот, на моих рисунках каждая черточка на прямой — это 1 см, от нуля до единицы их шесть.
Что такое 1/6? Это одна часть от шести частей. То есть, 1 см от 6 см. <рисунок1>
Луч длиной 1 см.
Что такое 1/3? Это одна часть от трёх частей.
Делим 6 см на три части, получается три части по 2 см. Чертим луч в 2 см, это 1/3. <рисунок2>
Что такое 1/2? Одна часть от двух частей, половина. Половина от шести будет три. Луч будет в 3 см. <рисунок3>
Что такое 3/6? Это три части от шести, три раза по 1/6 три раза по 1 см; 3/6 — это же и половина, это же 1/2, это же луч длиной в 3 см. <рисунок3>
Так, по аналогии, и с другими дробями:
1/6 — это луч длиной 1 см,
3/6 — это луч длиной 3 см,
5/6 — это луч длиной 5 см,
2/6 — это луч длиной 2 см,
1/3 — это луч длиной 2 см,
2/3 — это луч длиной 4 см,
1/2 — это луч длиной 3 см.
Проще говоря, можно умножить 6 (6 см, единичный отрезок, данный по условию задачи) на дробь и получить число (в см) , равное длине луча.
Например,
.
Некоторые лучи совпадают, это 3/6 и 1/2; 2/6 и 1/3. Потому что эти дроби равны. 3/6, если сократить, получится 1/2. 2/6 тоже сокращается до 1/3.