Войти Регистрация Спроси ai-bota

Размер (высота) типографического шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528мм. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А5 так же, как этот же текст, напечатанный шрифтом высотой 16 пунктов на листе формата А4? Размер шрифта округляется до целого.

Показать ответ

Ответ:

superdmnomber1

17.02.2020 12:37

#1.

$\frac{o-c}{c^2+o^2} * (\frac{c+o}{c} - \frac{2c}{c-0} ) = \frac{o-c}{c^2+o^2} * (\frac{(c-o)(c+o)-2c*c}{c(c-o)}) = \frac{o-c}{c^2+o^2} * (\frac{c^2-o^2-2c^2}{c(c-o)}) = \frac{(o-c)(-c^2-o^2)}{(c^2+o^2)*c(c-o)} =\\\\=\frac{(c-o)(c^2+o^2)}{(c^2+o^2)*c(c-o)} = \frac{1}{c}$

$c = 25\\\frac{1}{25} = 0,04$

ответ: 0,04.

#2.

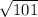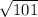$\sqrt{100} \leq \sqrt{101} \leq \sqrt{121} \\10 \leq \sqrt{101} \leq 11$

Первое число ( $\sqrt{101}$ ) правее числа 10.

$\sqrt{36} \leq \sqrt{41} \leq \sqrt{49} \\6 \leq \sqrt{41} \leq 7$

Второе число $(\sqrt{41})$ правее числа 6.

#3.

Рассчитаем размер скидки для дневного сеанса:

$188 * \frac{41}{100} = 77,08$

Найдем стоимость билета с дневной скидкой:

188-77,08 = 110,92 ≈ 111 руб.

Групповая скидка не будет применяться, так как она действует на группы больше 3 человек (от 4 и больше), поэтому ответ в обоих окошках будет одинаковый: 111 руб.

Также, так как сеанс дневной, то бонус не прилагается.

#4.

"Превышение установленной скорости движения" - 7 столбик - 2%

"Несоответствие скорости конкретным условиям движения" - 5 столбик - 5%

В сумме - (5+2) = 7% от всех происшествий

$184000 * \frac{7}{100} = \frac{184000*7}{100} = 1840 * 7 = 12880$

ответ: 12880.

#5.

Найдем значение y при x = 0

x = 0, y = 1

Получается, в формуле второе число будет 1;

Найдем первое число, назовем его z:

zx + 1 = y

Найдем значение x при y = 0:

y = 0; x = -2

Подставим эти значения в уравнение:

-2z + 1 = 0

2z = 1

z = 0,5

ответ: 0,5x + 1 = y

0,0(0 оценок)

Ответ:

Sunnnygirl289

17.02.2020 12:37

#1.

$\frac{o-c}{c^2+o^2} * (\frac{c+o}{c} - \frac{2c}{c-0} ) = \frac{o-c}{c^2+o^2} * (\frac{(c-o)(c+o)-2c*c}{c(c-o)}) = \frac{o-c}{c^2+o^2} * (\frac{c^2-o^2-2c^2}{c(c-o)}) = \frac{(o-c)(-c^2-o^2)}{(c^2+o^2)*c(c-o)} =\\\\=\frac{(c-o)(c^2+o^2)}{(c^2+o^2)*c(c-o)} = \frac{1}{c}$

$c = 25\\\frac{1}{25} = 0,04$

ответ: 0,04.

#2.

$\sqrt{100} \leq \sqrt{101} \leq \sqrt{121} \\10 \leq \sqrt{101} \leq 11$

Первое число ( $\sqrt{101}$ ) правее числа 10.

$\sqrt{36} \leq \sqrt{41} \leq \sqrt{49} \\6 \leq \sqrt{41} \leq 7$

Второе число $(\sqrt{41})$ правее числа 6.

#3.

Рассчитаем размер скидки для дневного сеанса:

$188 * \frac{41}{100} = 77,08$

Найдем стоимость билета с дневной скидкой:

188-77,08 = 110,92 ≈ 111 руб.

Групповая скидка не будет применяться, так как она действует на группы больше 3 человек (от 4 и больше), поэтому ответ в обоих окошках будет одинаковый: 111 руб.

Также, так как сеанс дневной, то бонус не прилагается.

#4.

"Превышение установленной скорости движения" - 7 столбик - 2%

"Несоответствие скорости конкретным условиям движения" - 5 столбик - 5%

В сумме - (5+2) = 7% от всех происшествий

$184000 * \frac{7}{100} = \frac{184000*7}{100} = 1840 * 7 = 12880$

ответ: 12880.

#5.

Найдем значение y при x = 0

x = 0, y = 1

Получается, в формуле второе число будет 1;

Найдем первое число, назовем его z:

zx + 1 = y

Найдем значение x при y = 0:

y = 0; x = -2

Подставим эти значения в уравнение:

-2z + 1 = 0

2z = 1

z = 0,5

ответ: 0,5x + 1 = y

0,0(0 оценок)

Популярные вопросы: Математика

taniabelkova

02.04.2022 23:12

Вычислите: i -0,72 i - i -0,2 i = ?...

gregoryan2001

02.04.2022 23:12

Если сложить уменьшаемое,вычитаемое и разность ,то получится 190.найдите каждое из них, если разность меньше уменьшаемого на 74....

Maowsk

30.08.2022 00:40

Собъяснениями в)1/2 и 1/7 ж)1/2 и 6/7 л)1/10 и 1/11 п)3/10 и 4/13 г)1/2 и 1/9 з)1/2 и 7/9 м)3/10 и 10/11 р)9/10 и 12/13 дроби к общему знаменателю равному произвед. знам. дробей...

Гули0203

30.08.2022 00:40

Сумма двух чисел равна 662.одно из чисел заканчивается на 0 . но если убрать этот 0 , то получается второе число .найдите эти числа...

Grinberg2003

30.08.2022 00:40

Найти изложение на татарском языке,сам не могу уже какой час ищу. название вроде бөркет , вот так начинается : безнең илдә каракошның җиде төре яши,ә аның иң күренеклесе элбэттэ бөркет.ул...

dog126

30.08.2022 00:40

Для строительства своего домика кум тыква собрал 82 кирпича из 35 кирпичей он хочет сделать первый этаж из 24 -второй,а из остальных кирпичей третий этаж дома сколько кирпичей останется...

austimenko291

30.08.2022 00:40

Количество чисел, кратных числу 2, которые можно получить, переставляя цифры числа 3279, равно...

babaevgleb70

30.08.2022 00:40

Вбидоне 40 литров молока. после того как молоком наполнили несколько трёхлитровых банок, в бидоне осталось 7 литров. сколько банок наполнили молоком...

MaxPlayTheme

30.08.2022 00:40

Водинаковыми буквами обозначены одинаковые цифры, разными буквами разные цифры. расшифруйте запись: три-два=ярд...

butterfly31

26.12.2021 20:15

Cрочно! a)7-4x 6x-23 b)2(3+-5x) _9 система)3x-2 x+4 x-4 6x+3 -2 2x-1 2...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку