49 см²
Пошаговое объяснение:
Вариант 1
Площадь прямоугольника - 14*7=98см²
Площадь прямоугольного треугольника считается по формуле = где a и b - катеты.
Катеты треугольников ABS и CDU равны 7 и 7 см (точки S и U - середина, значит катеты CU и AS равны 7 см).
Отсюда площадь треугольника = = 24.5 см²
Площадь двух треугольников = 24.5*2=49 см²
Значит площадь заштрихованной фигуры = 98-49=49 см²
Вариант 2 (в качестве альтернативного решения)
т.к. точки U и S - середина, то образуются квадратыUCDS и BUSA со стороной 7 см. Т.к. треугольники занимают ровно половину квадратов, то получаем:
площадь квадрата - 7*7=49см²
из них заштрихованная = 49/2=24,5см²
Площадь двух заштрихованных областей - 24,5*2=49см²
сначала находим критические точки (точки экстремумов)
это через первую производную
f'(x) = 3x²-3 = 3(х²-1)
3(х²-1)=0 ⇒ х₁ = 1; х₂ = -1
х₂ = -1 не входит в заданный отрезок. ее не рассматриваем
у нас есть одна точка экстремума и две точки - концы отрезка.
смотрим значение функции в этих точках
f(1/2) = -0.375
f(1) = -1
f(2) = 3
таким оразом
максимум функции f(x)=x³-3x+1 на отрезке [1/2, 2]
достигается на правом конце отрезка и равен f(2) = 3
минимум функции f(x)=x³-3x+1 на отрезке [1/2, 2]
достигается в точке локального минимума х₀= 1 и равен f(1) = -1
49 см²
Пошаговое объяснение:
Вариант 1
Площадь прямоугольника - 14*7=98см²
Площадь прямоугольного треугольника считается по формуле =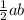
где a и b - катеты.
Катеты треугольников ABS и CDU равны 7 и 7 см (точки S и U - середина, значит катеты CU и AS равны 7 см).
Отсюда площадь треугольника =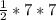
= 24.5 см²
Площадь двух треугольников = 24.5*2=49 см²
Значит площадь заштрихованной фигуры = 98-49=49 см²
Вариант 2 (в качестве альтернативного решения)
т.к. точки U и S - середина, то образуются квадратыUCDS и BUSA со стороной 7 см. Т.к. треугольники занимают ровно половину квадратов, то получаем:
площадь квадрата - 7*7=49см²
из них заштрихованная = 49/2=24,5см²
Площадь двух заштрихованных областей - 24,5*2=49см²
Пошаговое объяснение:
сначала находим критические точки (точки экстремумов)
это через первую производную
f'(x) = 3x²-3 = 3(х²-1)
3(х²-1)=0 ⇒ х₁ = 1; х₂ = -1
х₂ = -1 не входит в заданный отрезок. ее не рассматриваем
у нас есть одна точка экстремума и две точки - концы отрезка.
смотрим значение функции в этих точках
f(1/2) = -0.375
f(1) = -1
f(2) = 3
таким оразом
максимум функции f(x)=x³-3x+1 на отрезке [1/2, 2]
достигается на правом конце отрезка и равен f(2) = 3
минимум функции f(x)=x³-3x+1 на отрезке [1/2, 2]
достигается в точке локального минимума х₀= 1 и равен f(1) = -1