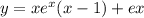Умножим обе части уравнения на , мы получим
Проинтегрируем обе части уравнения:
Интеграл в последнем уравнении стоящий справа решим по частям
Получили общее решение.
Найдём теперь частное решение, подставив начальные условия.
Частное решение:
Умножим обе части уравнения на , мы получим
, мы получим
Проинтегрируем обе части уравнения:
Интеграл в последнем уравнении стоящий справа решим по частям
Получили общее решение.
Найдём теперь частное решение, подставив начальные условия.
Частное решение: