Решение задачи Коши для дифференциального уравнения
второго порядка
y''-9y=9x, y(0)=0,y'(0)=0

Question

Математика: Решение задачи Коши для дифференциального уравнения второго порядка y -9y=9x, y(0)=0,y (0)=0

FRAIS11 · Answer

Решаем соответствующее однородное диф. уравнение

y'' - 9y = 0

Переходим к характеристическому уравнению

$k^2-9=0\\ k=\pm3$

Общее решение линейного однородного диф. уравнения

Yo.o =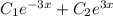 $C_1e^{-3x}+C_2e^{3x}$

Рассмотрим правую часть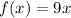 f(x)=9x . Частное решение будем искать в виде : Yч.н. =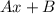 Ax+B

$y'=A\\ y''=0$

$-9(Ax+B)=9x\\ -9Ax-9B=9x$

Приравнивая коэффициент при степени x, мы получим

-9A = 9 откуда A = -1

-9B = 0 откуда B = 0

Следовательно, Yч.н. = -x

Y = Yo.o. + Yч.н. =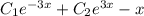 $C_1e^{-3x}+C_2e^{3x}-x$ - общее решение линейного неоднородного дифференциального уравнения.

$y'=-3C_1e^{-3x}+3C_2e^{3x}-1$

Найдём теперь задачу Коши, подставив начальные условия

$\displaystyle \left \{ {{C_1+C_2=0} \atop {-3C_1+3C_2-1=0}} \right. ~~\Rightarrow~~\left \{ {{C_1=-\dfrac{1}{6}} \atop {C_2=\dfrac{1}{6}}} \right.$

$\boxed{y=-\dfrac{1}{6}e^{-3x}+\dfrac{1}{6}e^{3x}-x}$