Реши уравнение с устный объяснением x*12=12. x: 9=0. 25: x= скоро в школу

Показать ответ

Ответ:

Eka228

13.09.2022 13:24

Если мы умножаем "минус" на "плюс", то получаем "минус".

Если мы умножаем "плюс" на "минус", то получаем "минус".

Если мы умножаем "минус" на "минус", то получаем "плюс".

Если мы умножаем "плюс" на "плюс", то получаем "плюс".

1.Вычислите сумму:

А) (−6)+(−3)=-6-3=-9;

Б) (−5)+(−6)=-5-6=-11;

В) (−47)+(−37)= -47-37=-84;

Г) (−63)+(−19)=-63-19=-82.

2.Подберите такое число, чтобы получилось верное равенство:

А) −6+(-2)=−8;

Б) −6+(-4)=−10;

В) (-10)+(−3)=−13;

Г) (-4)+(−3)=−7;

Д) (-1)+(−9)=−10;

Е) −2+(-2)=−4.

3.Вычислите сумму:

А) (−3)+(−7) =-3-7=-10;

Б) (−531)+(−834) =-531-834=-1365;

В) (−35)+(−19) =-35-19=-54;

Г) (−17)+(−101) =-17-101=-118;

Д) (+36)+(+14) =36+14=50;

Е) (+21)+(+14) =21+14=35;

Ж) (−28)+(−14) =-28-14=-42.

0,0(0 оценок)

Ответ:

DedMazaj

13.09.2022 13:24

Решать задачу будем в два этапа: сначала определим число разбить друзей на 3 пронумерованные команды, а затем учтем, что эта нумерация не важна.

1. Формируем первую команду. Туда должны попасть некоторые 3 человека из 9. Порядок их выбора не важен, поэтому выбрать их можно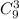 C_9^3 .

Формируем вторую команду. Туда должны попасть некоторые 3 человека из оставшихся 6. Порядок их выбора также не важен, поэтому выбрать их можно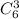 C_6^3 .

Оставшиеся 3 человека автоматически сформируют третью команду.

Поскольку каждому варианту первой команды можно поставить в соответствие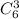 C_6^3 вариантов второй (и третьей) команды, то по правилу умножения всего разбить 9 человек на 3 пронумерованные команды:

$C_9^3\cdot C_6^3$

2. Теперь учтем тот факт, что у команд на самом деле нет номеров. Так как команд 3, то существует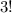 пронумеровать команды. Таким образом, количество непронумерованных вариантов разбиения в 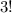раз меньше, чем количество пронумерованных вариантов разбиения.

Значит, итоговое число разбить 9 человек на команды без учета их номеров:

$\dfrac{C_9^3\cdot C_6^3}{3!} =\dfrac{\dfrac{9!}{3!\cdot(9-3)!} \cdot \dfrac{6!}{3!\cdot(6-3)!}}{3!} =\dfrac{9!\cdot 6!}{3!\cdot6!\cdot 3!\cdot3!\cdot3!}=\dfrac{9!}{(3!)^4}=$