1) Сначала определим количество выборов стульев для гостей.
Пусть из множество A берется сразу несколько элементов. В результате такого одновременного неупорядоченного выбора k элементов из множества A, состоящего из n элементов, получаются комбинации выбора), которые называются сочетаниями без повторений из n элементов по k (количество выбора).
Число сочетаний из n элементов по k обозначается и равно:
где m!=1·2·3·...·(m-1)·m.
Тогда, по условию задачи общее количество стульев n=8 и нужно выбрать стульев k=4:
2) Теперь определим количество рассадки 4-х гостей на 4-х стульях. Так как каждый вариант рассадки отличается только порядком участников, то есть является перестановкой из 4 элементов:
P₄=4!.
3) Количество необходимых для рассадки 4-х гостей на 8-ми стульях определим как произведения число сочетаний на перестановку:
». Какое-то время будущий писатель учился во второй одесской гимназии (впоследствии стала пятой). Одноклассником его в ту пору был Борис Житков (в будущем также писатель и путешественник), с которым у юного Корнея завязались дружеские отношения. Окончить гимназию Чуковскому так и не удалось: его отчислили, по его собственным утверждениям, из-за низкого происхождения[4][3]. Эти события он описал в автобиографической повести «Серебряный герб».
По метрике у Николая и его сестры Марии, как незаконнорождённых, не было отчества; в других документах дореволюционного периода его отчество указывалось по-разному — «Васильевич» (в свидетельстве о браке и крещении сына Николая, впоследствии закрепилось в большинстве поздних биографий как часть «настоящего имени»; дано по крёстному отцу), «Степанович», «Эммануилович», «Мануилович», «Емельянович»[5], сестра Маруся носила отчество «Эммануиловна» или «Мануиловна». С начала литературной деятельности Корнейчуков использовал псевдоним «Корней Чуковский», к которому позже присоединилось фиктивное отчество — «Иванович». После революции сочетание «Корней Иванович Чуковский» стало его настоящим именем, отчеством и фамилией[5].
По воспоминаниям К. Чуковского, у него «никогда не было такой роскоши, как отец или хотя бы дед», что в юности и в молодости служило для него постоянным источником стыда и душевных страданий[6].
Его дети — Николай, Лидия, Борис и умершая в детстве Мария (Мурочка), которой посвящены многие детские стихи отца — носили (по крайней мере, после революции) фамилию Чуковских и отчество Корнеевич/Корнеевна.
Пошаговое объяснение:
1) Сначала определим количество выборов стульев для гостей.
Пусть из множество A берется сразу несколько элементов. В результате такого одновременного неупорядоченного выбора k элементов из множества A, состоящего из n элементов, получаются комбинации выбора), которые называются сочетаниями без повторений из n элементов по k (количество выбора).
Число сочетаний из n элементов по k обозначается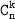
и равно:
где m!=1·2·3·...·(m-1)·m.
Тогда, по условию задачи общее количество стульев n=8 и нужно выбрать стульев k=4:
2) Теперь определим количество рассадки 4-х гостей на 4-х стульях. Так как каждый вариант рассадки отличается только порядком участников, то есть является перестановкой из 4 элементов:
P₄=4!.
3) Количество необходимых для рассадки 4-х гостей на 8-ми стульях определим как произведения число сочетаний на перестановку:
По метрике у Николая и его сестры Марии, как незаконнорождённых, не было отчества; в других документах дореволюционного периода его отчество указывалось по-разному — «Васильевич» (в свидетельстве о браке и крещении сына Николая, впоследствии закрепилось в большинстве поздних биографий как часть «настоящего имени»; дано по крёстному отцу), «Степанович», «Эммануилович», «Мануилович», «Емельянович»[5], сестра Маруся носила отчество «Эммануиловна» или «Мануиловна». С начала литературной деятельности Корнейчуков использовал псевдоним «Корней Чуковский», к которому позже присоединилось фиктивное отчество — «Иванович». После революции сочетание «Корней Иванович Чуковский» стало его настоящим именем, отчеством и фамилией[5].
По воспоминаниям К. Чуковского, у него «никогда не было такой роскоши, как отец или хотя бы дед», что в юности и в молодости служило для него постоянным источником стыда и душевных страданий[6].
Его дети — Николай, Лидия, Борис и умершая в детстве Мария (Мурочка), которой посвящены многие детские стихи отца — носили (по крайней мере, после революции) фамилию Чуковских и отчество Корнеевич/Корнеевна.