ИССЛЕДОВАНИЕ 1. Область определения. Деление на ноль в знаменателе. Х≠ 1. Х∈(-∞;0)∪(0;+∞) 2. Вертикальная асимптота: Х= 1. 3. Пересечение с осью Х. Y(x) = 0 - нет. 4. Пересечение с осью У - нет 5. Наклонная асимптота k = lim(+∞)Y(x)/x = 4*x/x = 4. Уравнение асимптоты: Y = 4*x.
6. Проверка на чётность. Y(-x) ≠ Y(x). Y(-x) ≠ - Y(x) Функция ни четная ни нечетная. 7. Поведение в точке разрыва. lim(->0-) Y(x) = -∞. lim(->0+) Y(x) = +∞ 8, Первая производная. 6. Локальные экстремумы. Y'(x) = 0, x1 = - 3/2, x2 = 3/2 Максимум Y(-3/2)= .-12.
Минимум Y(3/2) = 12. 7. Участки монотонности функции. Возрастает - Х∈(-∞;-3/2]∪[3/2;+∞).
Убывает - Х∈[-3/2;0)∪(0;3/2] 8. Вторая производная.
Корней нет. Точек перегиба (на графике) - нет. 9. Выпуклая - "горка" - Х∈(-∞;0). Вогнутая - "ложка" - Х∈(0;+∞)
Выражение: (4 - 14/33 * 1 1/21) * 5 5/8 содержит скобки, действие умножения, дроби.
Определяем порядок действий
Сначала всегда выполняются вычисления в скобках. Смотрим: в скобках у нас вычитание и умножение. По правилу, первым делается умножение. В нашем примере: 14/33 * 1 1/21.
Умножаем простую дробь на смешанную
Для этого смешанную дробь 1 1/21 переводим в неправильную: 1 представляем как 21/21 и прибавляем 1/21. Получается: 22/21.
Перемножаем 14/33 и 22/21.
По правилам, надо просто умножить числитель на числитель (14 * 22), знаменатель на знаменатель (33 * 21).
Но не всегда надо идти по этому пути, ведь в нашем случае цифры довольно громоздкие.
Поэтому смотрим, есть ли возможность их сократить. Видим, что числа 14 (в числителе) и 21 (в знаменателе) можно сократить на 7, а числа 33 (в знаменателе) и 22 (в числителе) можно сократить на 11. В результате в числителе остается 2 * 2, в знаменателе 3 * 3. Результат: 4/9.
Вторым действием в скобках будет: 4 – 4/9.
Вычитаем дробь из целого числа
Для этого представим число 4 как 3 9/9. И тогда:
3 9/9 – 4/9 = 3 5/9.
Наконец, последнее действие — умножение на 5 5/8.
Перемножим смешанные дроби
Алгоритм этого действия такой: смешанные дроби превращаем в неправильные и перемножаем числители и знаменатели.
3 5/9 переводим в неправильную:
3 * 9 = 27;
27 + 5 = 32 (это и будет числитель).
Результат: 32/9.
5 5/8 переводим в неправильную:
5 * 8 = 40;
40 + 5 = 45 (это и будет числитель).
Результат: 45/8.
Теперь перемножаем 32/9 и 45/8.
Видно, что тут можно сократить 32 и 8 на 8, а 9 и 45 — на 9.
ДАНО
Y = (x² + 9)/x
ИССЛЕДОВАНИЕ
1. Область определения. Деление на ноль в знаменателе.
Х≠ 1.
Х∈(-∞;0)∪(0;+∞)
2. Вертикальная асимптота: Х= 1.
3. Пересечение с осью Х. Y(x) = 0 - нет.
4. Пересечение с осью У - нет
5. Наклонная асимптота
k = lim(+∞)Y(x)/x = 4*x/x = 4. Уравнение асимптоты: Y = 4*x.
6. Проверка на чётность.
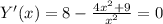
Y(-x) ≠ Y(x). Y(-x) ≠ - Y(x)
Функция ни четная ни нечетная.
7. Поведение в точке разрыва.
lim(->0-) Y(x) = -∞.
lim(->0+) Y(x) = +∞
8, Первая производная.
6. Локальные экстремумы.
Y'(x) = 0, x1 = - 3/2, x2 = 3/2
Максимум Y(-3/2)= .-12.
Минимум Y(3/2) = 12.
7. Участки монотонности функции.
Возрастает - Х∈(-∞;-3/2]∪[3/2;+∞).
Убывает - Х∈[-3/2;0)∪(0;3/2]
8. Вторая производная.
Корней нет. Точек перегиба (на графике) - нет.
9. Выпуклая - "горка" - Х∈(-∞;0). Вогнутая - "ложка" - Х∈(0;+∞)
10. График в приложении
Задать вопрос
Войти
banner background
АнонимМатематика15 августа 01:53
Найдите значение выражение (4-14/33×1 1/21)×5 5/8
РЕКЛАМА
Выгодно с картой "Мир" на mos.ru
Перейти
ответ или решение2
Фадеев Макар
Выражение: (4 - 14/33 * 1 1/21) * 5 5/8 содержит скобки, действие умножения, дроби.
Определяем порядок действий
Сначала всегда выполняются вычисления в скобках. Смотрим: в скобках у нас вычитание и умножение. По правилу, первым делается умножение. В нашем примере: 14/33 * 1 1/21.
Умножаем простую дробь на смешанную
Для этого смешанную дробь 1 1/21 переводим в неправильную: 1 представляем как 21/21 и прибавляем 1/21. Получается: 22/21.
Перемножаем 14/33 и 22/21.
По правилам, надо просто умножить числитель на числитель (14 * 22), знаменатель на знаменатель (33 * 21).
Но не всегда надо идти по этому пути, ведь в нашем случае цифры довольно громоздкие.
Поэтому смотрим, есть ли возможность их сократить. Видим, что числа 14 (в числителе) и 21 (в знаменателе) можно сократить на 7, а числа 33 (в знаменателе) и 22 (в числителе) можно сократить на 11. В результате в числителе остается 2 * 2, в знаменателе 3 * 3. Результат: 4/9.
Вторым действием в скобках будет: 4 – 4/9.
Вычитаем дробь из целого числа
Для этого представим число 4 как 3 9/9. И тогда:
3 9/9 – 4/9 = 3 5/9.
Наконец, последнее действие — умножение на 5 5/8.
Перемножим смешанные дроби
Алгоритм этого действия такой: смешанные дроби превращаем в неправильные и перемножаем числители и знаменатели.
3 5/9 переводим в неправильную:
3 * 9 = 27;
27 + 5 = 32 (это и будет числитель).
Результат: 32/9.
5 5/8 переводим в неправильную:
5 * 8 = 40;
40 + 5 = 45 (это и будет числитель).
Результат: 45/8.
Теперь перемножаем 32/9 и 45/8.
Видно, что тут можно сократить 32 и 8 на 8, а 9 и 45 — на 9.
Остается: 4/1 * 5/1 = 20.
ответ: 20.