решить 1)2ав-3в,если а=2,в=3
2)ав-3а+1,если а=1,в=2
3)1,8×2,4-1,8×4,4+1
4)3,1×1,4-3,1×2,4+2
5)2х-(3х+у)+2
6)х-(2х-3у)-3(у-1)+2х

Показать ответ

Ответ:

antonlutsenko1

10.01.2021 18:48

По тарифу "Летний"

Пошаговое объяснение:

По формуле сложного процента общая сумма которую получит вкладчик по тарифу "Летний"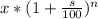 $x *(1+\frac{s}{100} )^n$ где x - начальная сумма, n- количество месяцев, s% - месячная ставка в процентах

Считаем: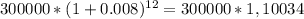 $300000*(1+0.008)^{12} = 300000 * 1,10034$

Т.е. дополнительно вкладчик получит 10,034%

Для тарифа классический все просто: по истечении года он получит 9.8%

10% > 9.8%, поэтому по тарифу "Летний" вкладчик получит большую сумму

============

Не забывайте нажать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"

Успехов в учебе

0,0(0 оценок)

Ответ:

Haroojul

26.08.2022 13:29

ответ: a∈(-1;-2/3) ∪ (-2/3 ; -1/3)

Пошаговое объяснение:

ОДЗ: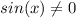 $sin(x) \neq 0$

Используем формулу:

$ctg^2(x) = \frac{1}{sin^2(x)} -1$

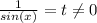
Замена: $\frac{1}{sin(x)} = t\neq 0$

$(1+a)(t^2-1) -(2a+4)t +1-7a = 0\\(1+a)t^2 -(2a+4)t -8a =0$

Заметим, что для того чтобы существовало одно решение на интервале (0;π/2), необходимо и достаточно, чтобы выполнялось условие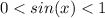 , в этом случае на промежутке (0;π/2) будет существовать ровно ОДНО значение x, в противном случае, решений на данном промежутке не будет.

Откуда, должно выполнятся условие: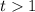

По условию, нужно найти те значения параметра a, при которых будет более одного решения на интервале (0;π/2), а значит данное уравнение должно иметь как минимум два положительных решения.

Рассмотрим линейный случай, ибо может быть бесконечное число решений: a=-1

-2t-8a = 0 - одно решение

2) Основной случай.

Должно быть два корня, каждый из которых больше единицы :

$(1+a)t^2 -(2a+4)t -8a =0\\\frac{D}{4} = (a+2)^2 +8a(1+a) = 9a^2+12a+4 = (3a+2)^20\\ a\neq-\frac{2}{3} \\t_{1} = \frac{a+2+3a+2}{1+a}=41 \\t_{2} = \frac{a+2-3a-2}{1+a} 1\\\frac{-2a}{1+a} 1\\\frac{3a+1}{a+1} < 0\\ \left \{ -1$