решить 1)Найти закон распределения дискретной случайности величины,если известно,что:дискретная случайная величина X может принимать только два значения x1 и x2,причем x1 P1=0.1 M(x)=3.9 D(x)=0.09
2)найти общее решение (общий интеграл)дифференциального уравнения I порядка
Y`=x+8y/8x+y
3)задан закон s(t) изменения пути движения материальной точки;нужно найти значения скорости и ускорения этой точки в момент времени t0:
s(t)=2t^4-3t^2+t-2 t0=2
ответ:Сначала найдем саму функцию вида у=ax^2+bx+с, заменив переменные a, b и c числами. Для этого подставляем известные значения х и у:
а*0+b*0+с=4, отсюда находим с=4
a*1+b*1+4=-1, отсюда находим а=-5-b
(-5-b)*4+b*2+4=-4, отсюда находим b=-6 и подставляя это значение во второе уравнение находим, что a=1
Теперь ищем ее вершину:
По формуле вершин для парабол: х=-b/2a; y=(b^2-4ac)/4a, отсюда находим х=-((-6)/2*1)=3; у=-(((-6)^2-4*1*4)/(4*1))=-5
Альтернативно можно было бы решить через производную, результат бы не изменился.
ответ: координатой вершины является точка(3|-5).
Пошаговое объяснение:
1 - 63. 2 - 81. 3 - 66
Пошаговое объяснение:
Количество помидоров в первом ящике - 30% от 210 = 63кг
Кол-во помидоров на 2 и 3 ящик - 210-63=147
Можно решить данную задачу уравнением.
Пусть х - кол-во помидоров в 3 ящике, тогда во втором будет 1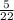
х. Общее кол-во помидоров - 147. Составляем уравнение:
1 5/22x + x = 147
27/22x+x=147
умножим обе части на 22/49 чтобы избавиться от дроби
x = 22*3
x = 66
Так мы получили, что в 3 ящике 66 кг помидоров. Во втором - 66* 1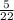
= 15 (это на столько больше) 66+15=81.