Числитель первой дроби положителен, а вот ее знаменатель отрицателен. Увидеть это можно либо использовав формулу суммы, либо заметив, что и поскольку синус возрастает на , то и . Значит, эта дробь отрицательна.
Числитель второй дроби очевидно положителен, как и ее знаменатель: . Значит, эта дробь положительна.
Числитель первой дроби положителен, а вот ее знаменатель отрицателен. Увидеть это можно либо использовав формулу суммы, либо заметив, что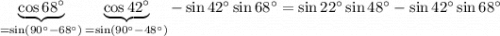 и поскольку синус возрастает на
и поскольку синус возрастает на 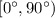 , то
, то 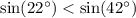 и
и 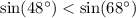 . Значит, эта дробь отрицательна.
. Значит, эта дробь отрицательна.
Числитель второй дроби очевидно положителен, как и ее знаменатель: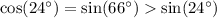 . Значит, эта дробь положительна.
. Значит, эта дробь положительна.