Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
klara90
13.01.2021 06:50 •
Математика
Решить диф.ур.
Показать ответ
Ответ:
sashgrts
10.10.2020 23:50
После замены
и с учетом
вы получите
Выполнив обратную замену, мы получим
Получили общий интеграл
0,0
(0 оценок)
Популярные вопросы: Математика
nk9696
11.05.2022 06:39
Каждый из 5 учащихся собрала 6 ящиков яблок было собрано еще 3 ящиков сколько всего ящиков яблок было собрано...
Ученая13
11.05.2022 06:39
На молочной ферме надо или за день 1680кг молока.одну восьмую всего молока переработала на сметану,одну треть сметаны-на масло.сколько килограммов молока переработали на масло...
livr5
11.05.2022 06:39
Надо выражение (√a-2√b)(√a+2√b)+4b...
Imdoingfinetoday123
11.05.2022 06:39
Вычислите 3/5*1/2*4/9, 4/5*10/27*10/16 расписать решение....
gamer2222
11.05.2022 06:39
Нужна ваша вот какой ответ у примеров: 744: 24,900: 450 напишите ответ и проверку...
manovskidominik
11.05.2022 06:39
Выступление ансамбля продолжалось 01: 44 и закончилось в 16: 29 минут. в котором часу началось выступление?...
Lenin227
11.05.2022 06:39
В году в нашем городе построили 4 дома по 62 квартир и 7 домов по 90 квартир сколько всего квартир в этих домах...
Animashka11
11.05.2022 06:39
Найди: 1/6 разности чисел92и 14 ; 1/4 произведения чисел 16 и 6;...
vaki3
11.05.2022 06:39
Найдите величену если 1% от этой величены 5мм и 3900 книг и 14мм и 7,3кг и 49,5тг и 1га...
milanakalinovskaya
11.05.2022 06:39
Турист за первый день 18 км что составляют 6 пятых пути который он должен пройти во 2й день сколько км должен пройти турист за оба дня вместе...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
После замены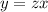 и с учетом
и с учетом 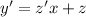 вы получите
вы получите
Выполнив обратную замену, мы получим
Получили общий интеграл