Математика: Решить дифференциальные уравнения

Решить дифференциальные уравнения

Показать ответ

Ответ:

GoldenLynx1999

10.10.2022 21:00

Решение .

Собственная скорость теплохода = х км/ч , а скорость течения

реки = у км/ч .

Скорость теплохода по течению = (х+у) км/ч .

Скорость теплохода против течения = (х-у) км/ч .

Расстояние между портами S=336 км

Время, затраченное теплоходом на прохождение этого расстояния по течению, равно 336/(x+y)=6 ч .

Время, затраченное теплоходом на прохождение этого расстояния против течения, равно 336/(x-y)=7 ч .

Решим систему уравнений .

$\left\{\begin{array}{l}\dfrac{336}{x+y}=6\\\, \dfrac{336}{x-y}=7\end{array}\right\ \ \left\{\begin{array}{l}336=6(x+y)\\336=7(x-y)\end{array}\right\ \ \left\{\begin{array}{l}x+y=56\\x-y=48\end{array}\right\ \oplus \ominus \ \left\{\begin{array}{l}2x=104\\2y=8\end{array}\rightleft\{\begin{array}{l}x=52\\y=4\end{array}\right$

ответ: скорость теплохода = 52 км/ч , скорость течения = 4 км/ч .

0,0(0 оценок)

Ответ:

yanbalan19

11.01.2021 23:31

1) Построим график функции у = √х
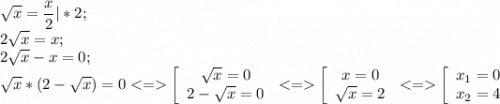
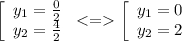
Мы знаем, что подкоренное выражение всегда больше или равно нулю, т.е. х ≥ 0 из чего следует что и у ≥ 0
Строим график(см. вложение)
2) Построим график функции x-2y = 0
Сначала выразим у из функции
x-2y = 0
2у = х |:2
у = х/2
Строим график(см. вложение)
3) Найдём точки пересечения графиков
Из рисунка видно, что они пересекаются в точках (0;0) и (4;2). Проверим это аналитически
У функций равны левые части ⇒ равны и правые
$\displaystyle \sqrt{x} =\frac{x}{2}|*2;\\2\sqrt{x} =x;\\2\sqrt{x} -x=0;\\\sqrt{x} *(2-\sqrt{x} )=0 < = \left[\begin{array}{ccc}\sqrt{x} =0\\2-\sqrt{x} =0\\\end{array}\right. < = \left[\begin{array}{ccc}x =0\\\sqrt{x} =2\\\end{array}\right. < = \left[\begin{array}{ccc}x_1 =0\\x_2=4\\\end{array}\right$
Теперь подставим значения х в любое выражение
$\displaystyle \left[\begin{array}{ccc}y_1 = \frac{0}{2} \\y_2 = \frac{4}{2} \\\end{array}\right. < = \left[\begin{array}{ccc}y_1 = 0\\y_2 = 2\\\end{array}\right.$
Получились те же точки (0;0) и (4;2).