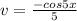1)
2)
Пошаговое объяснение:
Для нахождения интеграла нужно использовать формулу интегрирования по частям:
где ,
Нужно найти дифференциал , используя , вычислить при и подставить и
1)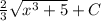
2)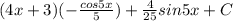
Пошаговое объяснение:
1)
2)
Для нахождения интеграла нужно использовать формулу интегрирования по частям:
где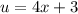 ,
, 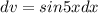
Нужно найти дифференциал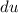 , используя
, используя 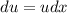 , вычислить
, вычислить  при
при 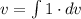 и подставить
и подставить 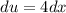 и
и