Для начала поработаем со вторым выражением. Первые три слагаемых свернем в квадрат разности: ; В следующих двух слагаемых вынесем общий множитель "40": ; В итоге получим следующее уравнение: . В скобках мы видим похожие выражения, отличающиеся лишь знаком посередине (такие выражение называются сопряженными). А хотелось бы видеть там равные (строго говоря тождественные) выражения. Пусть в первой скобке вместо будет стоять ; Это приведет к тому, что придется убавить ; В итоге: ; Слева стоит квадрат суммы. Уравнение примет вид: ; Сворачивая еще раз: ; Получаем серию прямых: ; А теперь приступим к рассмотрению первого уравнения.
Это уравнение задает круг с центром в точке (0, 0) и радиусом ; Рассмотрим прямую ; Найдем радиус окружности с центром в начале координат, которая касается данной прямой. Это легко сделать из подобия треугольников. ; Значит, круг касается всех этих четырех прямых. Достаточно найти только координаты касания с любой из прямых. Это делается так же, как и находился радиус окружности. Для той же прямой это координаты ; Ну а все решения:
В 30-х годах века военное ведомство США поручило Гарвардскому и Принстонскому университетам разработать электромеханическую вычислительную систему для военно-морской артиллерии. Результатом усилий этих университетов стали две концепции построения вычислительных систем, которые определили развитие мировой вычислительной техники почти на 100 лет вперед. Мы знаем их как гарвардская и принстонская (более известная как фон-неймановская) архитектуры
Их основное отличие заключалось в том, что архитектура фон Неймана использовала единую память (общую шину данных), а гарвардская предполагала наличие нескольких шин (в оригинале две: шина данных и шина команд).
Преимущества машины фон Неймана оценили сразу, поскольку в ней содержалось значительно меньше проводников между арифметико-логическим устройством (АЛУ) и областью памяти, и на долгие годы она стала эталоном для создания ВС. Именно фон-неймановская архитектура с подачи Джона Кока являлась прародителем процессоров RISC (Reduced Instruction Set Computer – вычисления с сокращенным набором команд).
Время шло, и в 70-х годах века появились полупроводники, в которых можно было создавать сотни микроскопических проводников. Проблема множества контактов была снята, и наступила эра гарвардской архитектуры. Действительно, если процессор имеет несколько шин, он может одновременно выполнить несколько действий. В этом случае за один такт гарвардский процессор может выполнить несколько операций, существенно опередив попроизводительности аналогичный фон-неймановский процессор. Чтобы это понять, достаточно посмотреть на схемы двух архитектур.Появление процессоров на гарвардской архитектуре мировое сообщество восприняло прохладно, поскольку в начале 70-х годов не было программного обеспечения реализовать его потенциал. Их за глаза называли процессорами «для бедных», поскольку они не могли работать на больших частотах.
Но все изменилось после появления персонального компьютера Apple I, в основе которого был восьмиразрядный процессор MOS 6502 на гарвардской архитектуре с операционной системой Apple DOS.
Простота ОС компенсировалась достаточно сложным процессором, названным впоследствии CISC (Complex Instruction Set Computer – вычисления с комплексным набором команд), с отдельной 16-разрядной адресной шиной ивозможностью произвольного манипулирования регистрами. Монолитная однопользовательская ОС позволила выжать из него небывалую по тем временам производительность при решении отдельных задачах.
Через несколько лет корпорация IBM бросилась догонять Apple, практически повторив ее идею. В основе созданного ею персонального компьютера (более известного нам как IBM-PC) были гарвардский процессор фирмы Intel и ОС Microsoft DOS. Впоследствии такие комплексы получили общеизвестную аббревиатуру – Wintel.
Естественно, что за скорость CISC-процессора приходилось платить удвоенным/утроенным количеством контактов, что не только перегревало процессор, но и накладывало ограничения на его размеры. В среднем на каждые 20% прироста производительности потребляемая мощность гарвардского процессора увеличивалась до 50%.
Выходом из этой ситуации стало появление многоядерных процессоров, в которых частота работы каждого вычислительного ядра была понижена, но суммарная производительность превышала даже показатели разогнанного одноядерного. Для наглядности на рис. 2 показан пример того, как меняются производительность и энергопотребление центрального процессора при изменении частот и количества ядер.
Для начала поработаем со вторым выражением. Первые три слагаемых свернем в квадрат разности: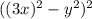
; В следующих двух слагаемых вынесем общий множитель "40": 
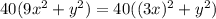; В итоге получим следующее уравнение: 
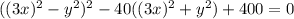. В скобках мы видим похожие выражения, отличающиеся лишь знаком посередине (такие выражение называются сопряженными). А хотелось бы видеть там равные (строго говоря тождественные) выражения. Пусть в первой скобке вместо 
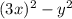будет стоять 
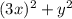; Это приведет к тому, что придется убавить 
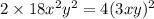; В итоге: 
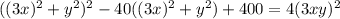; Слева стоит квадрат суммы. Уравнение примет вид: 
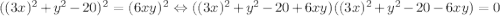; Сворачивая еще раз: 
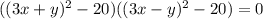; Получаем серию прямых: 
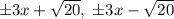; А теперь приступим к рассмотрению первого уравнения.
Это уравнение задает круг с центром в точке (0, 0) и радиусом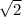
; Рассмотрим прямую 
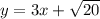; Найдем радиус окружности с центром в начале координат, которая касается данной прямой. Это легко сделать из подобия треугольников. 
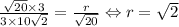; Значит, круг касается всех этих четырех прямых. Достаточно найти только координаты касания с любой из прямых. Это делается так же, как и находился радиус окружности. Для той же прямой это координаты 
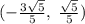; Ну а все решения:
Их основное отличие заключалось в том, что архитектура фон Неймана использовала единую память (общую шину данных), а гарвардская предполагала наличие нескольких шин (в оригинале две: шина данных и шина команд).
Преимущества машины фон Неймана оценили сразу, поскольку в ней содержалось значительно меньше проводников между арифметико-логическим устройством (АЛУ) и областью памяти, и на долгие годы она стала эталоном для создания ВС. Именно фон-неймановская архитектура с подачи Джона Кока являлась прародителем процессоров RISC (Reduced Instruction Set Computer – вычисления с сокращенным набором команд).
Время шло, и в 70-х годах века появились полупроводники, в которых можно было создавать сотни микроскопических проводников. Проблема множества контактов была снята, и наступила эра гарвардской архитектуры. Действительно, если процессор имеет несколько шин, он может одновременно выполнить несколько действий. В этом случае за один такт гарвардский процессор может выполнить несколько операций, существенно опередив попроизводительности аналогичный фон-неймановский процессор. Чтобы это понять, достаточно посмотреть на схемы двух архитектур.Появление процессоров на гарвардской архитектуре мировое сообщество восприняло прохладно, поскольку в начале 70-х годов не было программного обеспечения реализовать его потенциал. Их за глаза называли процессорами «для бедных», поскольку они не могли работать на больших частотах.
Но все изменилось после появления персонального компьютера Apple I, в основе которого был восьмиразрядный процессор MOS 6502 на гарвардской архитектуре с операционной системой Apple DOS.
Простота ОС компенсировалась достаточно сложным процессором, названным впоследствии CISC (Complex Instruction Set Computer – вычисления с комплексным набором команд), с отдельной 16-разрядной адресной шиной ивозможностью произвольного манипулирования регистрами. Монолитная однопользовательская ОС позволила выжать из него небывалую по тем временам производительность при решении отдельных задачах.
Через несколько лет корпорация IBM бросилась догонять Apple, практически повторив ее идею. В основе созданного ею персонального компьютера (более известного нам как IBM-PC) были гарвардский процессор фирмы Intel и ОС Microsoft DOS. Впоследствии такие комплексы получили общеизвестную аббревиатуру – Wintel.
Естественно, что за скорость CISC-процессора приходилось платить удвоенным/утроенным количеством контактов, что не только перегревало процессор, но и накладывало ограничения на его размеры. В среднем на каждые 20% прироста производительности потребляемая мощность гарвардского процессора увеличивалась до 50%.
Выходом из этой ситуации стало появление многоядерных процессоров, в которых частота работы каждого вычислительного ядра была понижена, но суммарная производительность превышала даже показатели разогнанного одноядерного. Для наглядности на рис. 2 показан пример того, как меняются производительность и энергопотребление центрального процессора при изменении частот и количества ядер.