Пошаговое объяснение:
Дифференциал работы - это скалярное произведение вектора силы на дифференциал перемещения:
При этом мы знаем, что , то есть
Итоговое выражение для работы:
Пошаговое объяснение:
Дифференциал работы - это скалярное произведение вектора силы на дифференциал перемещения:
При этом мы знаем, что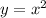 , то есть
, то есть 
Итоговое выражение для работы: