x∈∪
Пошаговое объяснение:
Преобразовываем выражение:
Находим нули каждого множителя:
По методу интервалов решением неравенства является промежуток:
∪
x∈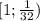 ∪
∪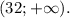
Пошаговое объяснение:
Преобразовываем выражение:
Находим нули каждого множителя:
По методу интервалов решением неравенства является промежуток: