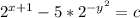Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
odinokijcelovek
06.09.2022 14:36 •
Математика
решить, ничего ни понимаю(
Решить дифференциальное уравнение первого порядка.
Показать ответ
Ответ:
ulagrac8
12.10.2020 15:14
Отдельно считаем левый интеграл
Вернемся к условию, получим, что:
ответ:
0,0
(0 оценок)
Популярные вопросы: Математика
qidanabala
10.11.2021 23:55
До різниці чисел 829 і 734 додати суму чисел 593 і 17...
shabishka
10.11.2021 23:55
Найдите все натуральные значения a, при которых одновременно дробь a/4 будет неправельной, а дробь a/9 правельной...
Zanyt
08.04.2021 01:45
А=100м собрали-? м2 2/5часть осталось-? м2...
lollo2003
08.04.2021 01:45
Найдите число, если 1/3 этого числа равна 19. найдите число, если 4/7 этого числа равны 1 11/21....
SiperV2
08.04.2021 01:45
Как школьнику предотвратить эскалацию конфликта в ситуации? какие навыки самоконтроля применить? во время перерыва в дверях столовой оттолкнули, чтобы стать первым в очереди...
NoMatterWho2001
08.04.2021 01:45
Света купила 6 карандашей по цене x руб. за карандаш, а таня купила 4 ручки по цене в 1,5 раза выше, чем цена за карандаш. после этого у девочек осталось 48,3 руб. какая сумма денег...
anastasiyanast29
08.04.2021 01:45
1.как зависит изготовления отливок от области их применения, класса точности и чистоты поверхности? 2.как производится планировка оборудования в механических цехах? 3.какие существуют...
LizaDemidova3101
08.04.2021 01:45
Запишите в виде десятичной дроби 7-10 27-100 574-1000 21 целая 8-10 9 целых 83-100...
alenazayka200
08.04.2021 01:45
Написать анализ стиха гора францишак багушевич как можно больше инфы,про рифму,героев,свое впечатление...
hocoladka
08.04.2021 01:45
Девочка прочитала книгу за 3дня. в первый день она прочитала 3/10 всей книги во второй 2/5 всей книги а в трерий остальные 96 страницы...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Отдельно считаем левый интеграл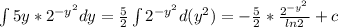
Вернемся к условию, получим, что:
ответ: