Проверим, может ли при каких-то a и b из G получиться в результате операции число не из G (то есть -1, так как, очевидно, результат операции - действительное число)
То есть посредством операции нельзя выйти из R\{-1}
Найдем нейтральный элемент по этой операции:
- нейтральный элемент существует
Проверим свойство ассоциативности:
- выполнено
Посмотрим, у каждого ли есть обратный элемент. Рассмотрим произвольный элемент a:
Обратный существует (так как a не равен -1), а также , то есть значение выражения для t не может быть -1, а отсюда t лежит в G.
ответ: первый автомобиль был в пути 6 часов,
второй автомобиль был в пути 8 часов.
Пошаговое объяснение:
1) пусть первый автомобиль был в пути х часов.
2) второй автомобиль был в пути (х+2) часов.
3) скорость первого автомобиля 360/х.
3) скорость второго автомобиля 480/(x+2).
4) так как скорости автомобилей равны ⇒
480/(x+2)=360/x
480*х=360*(х+2)
480x=360x+720
480х-360х=720
120x=720 |÷120
x=6.
6+2=8.
Заметим для начала, что операция коммутативна
Проверим, может ли при каких-то a и b из G получиться в результате операции число не из G (то есть -1, так как, очевидно, результат операции - действительное число)
То есть посредством операции нельзя выйти из R\{-1}
Найдем нейтральный элемент по этой операции:
Проверим свойство ассоциативности:
Посмотрим, у каждого ли есть обратный элемент. Рассмотрим произвольный элемент a:
Обратный существует (так как a не равен -1), а также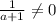
, то есть значение выражения для t не может быть -1, а отсюда t лежит в G.
Таким образом, G - абелева группа.