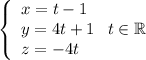Все легко! Карлсон очень любит ходить по крышам. И вот как то раз с одной крыши он увидел в доме грудного ребенка. Ребенок лежал и плакал. Родителей рядом небыло. Карлсон полетел к Малышу и спросил кто лучшия в мире нянька. Он конечно ответил что Карлсон. Карлсон полетел забрал ребеночка и принес к себе в домик на крышу, там он дал ему бутылочку... . Пока карлсон летал к малышу ребенок подрос спрыгнул с кровати и стащил у карлсона весь запас колбасу. Карлсон подумал что если у этого ребенка есть родители то их надо проучить...
Дальше сама разберешься. И вообще про это в повести уже написанно посмотри в книге или в интернете.
Вектор нормали найдём из векторного произведения векторов a и M₁M₂
Плоскость задаётся уравнением:
(x - 2) + 0(y - 2) - (z - 1) = 0
ответ: x - z - 1 = 0
2.
Чтобы записать уравнение прямой в каноническом и параметрическом виде необходимо найти направляющий вектор этой прямой и точку, через которую эта прямая проходит
Найдём координаты точки A, которая принадлежит прямой
Пусть z = 0
Решим систему:
Координаты точки A(-1, 1, 0)
Найдём координаты точки B, которая принадлежит прямой
Карлсон очень любит ходить по крышам. И вот как то раз с одной крыши он увидел в доме грудного ребенка. Ребенок лежал и плакал. Родителей рядом небыло. Карлсон полетел к Малышу и спросил кто лучшия в мире нянька. Он конечно ответил что Карлсон. Карлсон полетел забрал ребеночка и принес к себе в домик на крышу, там он дал ему бутылочку... . Пока карлсон летал к малышу ребенок подрос спрыгнул с кровати и стащил у карлсона весь запас колбасу. Карлсон подумал что если у этого ребенка есть родители то их надо проучить...
Дальше сама разберешься. И вообще про это в повести уже написанно посмотри в книге или в интернете.
1.
Уравнение плоскости, проходящей через некоторую точку с координатами (x₀,y₀,z₀), в общем виде записывается так:
A(x-x₀) + B(y-y₀) + C(z-z₀)= 0, где коэффициенты A,B,C - координаты вектора нормали
Найдём вектор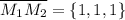
Вектор нормали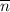 найдём из векторного произведения векторов a и M₁M₂
найдём из векторного произведения векторов a и M₁M₂
Плоскость задаётся уравнением:
(x - 2) + 0(y - 2) - (z - 1) = 0
ответ: x - z - 1 = 0
2.
Чтобы записать уравнение прямой в каноническом и параметрическом виде необходимо найти направляющий вектор этой прямой и точку, через которую эта прямая проходит
Найдём координаты точки A, которая принадлежит прямой
Пусть z = 0
Решим систему: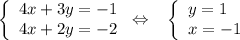
Координаты точки A(-1, 1, 0)
Найдём координаты точки B, которая принадлежит прямой
Пусть z = -4
Снова решим систему: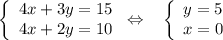
Координаты точки B(0, 5, -4)
Найдём направляющий вектор прямой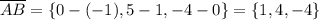
Запишем уравнение прямой в каноническом виде: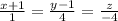
И в параметрическом виде: