Заменим набор данный набор чисел на остатки от деления на 2, которые дают числа набора. Числа у нас разбиты на пары , коих всего 7. Поскольку всего чисел в наборе 7, то либо только 1, либо только 0 нечетное количество. Примем без ограничения общности, что 1 нечетное количество. Тогда найдется хотя бы одна пара , в которой оба числа нечетны. Но в таком случае число четно, и произведение четно.
ответ: четно.
Пусть рассматривается число . Увеличенные на 1 некоторые последние цифры числа отличаются по четности от . Поэтому их сумма с рассматриваемым числом нечетна, значит, числа из 4 получиться не могло.
ответ: нет.
Посчитаем общее количество партий. Число 10+15+17=42 равно удвоенному количеству партий (поскольку, партия, сыгранная, скажем, между Кроликом и Алисой учитывается как в числе 10, так и в числе 17 ровно один раз, итого мы дважды посчитали одну и ту же партию). Значит, всего было сыграна 21 партия.
Заметим, что если игрок проигрывает все матчи, то он играет в каждой второй игре. Поэтому худший игрок сыграет хотя бы матчей (причем 10 в том случае, если он начал играть во второй игре и проиграл). Ровно столько сыграла Алиса. Заключаем, что она начала во второй игре и проиграла все матчи. Значит, проиграла и во второй партии.
Доказать конгруэнтность этих треугольников можно по признаку УСУ (угол, сторона, угол). Вот теорема:
Если два угла и сторона между ними одного треугольника равны двум углам и стороне между ними другого треугольника, то эти треугольники конгруэнтны (равны).
1) Нам говорят, что отрезок AD является биссектрисой угла BАC. Это означает, что:
Угол ВАD = Угол DAC.
2) Также нам говорят в условии, что угол ADB равняется углу ADC. Угол АDB = Угол ADC.
3) АD является общей стороной этих двух треугольников.
Значит два угла и сторона между ними одного треугольника равны двум углам и стороне между ними другого треугольника, и согласно этому признаку, мы можем сказать, что эти два треугольника конгруэнтны (равны друг-другу).
Заменим набор данный набор чисел на остатки от деления на 2, которые дают числа набора. Числа у нас разбиты на пары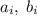
, коих всего 7. Поскольку всего чисел в наборе 7, то либо только 1, либо только 0 нечетное количество. Примем без ограничения общности, что 1 нечетное количество. Тогда найдется хотя бы одна пара 
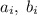, в которой оба числа нечетны. Но в таком случае число 
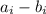четно, и произведение четно.
ответ: четно.
Пусть рассматривается число
. Увеличенные на 1 некоторые последние цифры числа отличаются по четности от 
. Поэтому их сумма с рассматриваемым числом нечетна, значит, числа из 4 получиться не могло.
ответ: нет.
Посчитаем общее количество партий. Число 10+15+17=42 равно удвоенному количеству партий (поскольку, партия, сыгранная, скажем, между Кроликом и Алисой учитывается как в числе 10, так и в числе 17 ровно один раз, итого мы дважды посчитали одну и ту же партию). Значит, всего было сыграна 21 партия.
Заметим, что если игрок проигрывает все матчи, то он играет в каждой второй игре. Поэтому худший игрок сыграет хотя бы![[21/2]=10](/tpl/images/1358/1826/6f35f.png)
матчей (причем 10 в том случае, если он начал играть во второй игре и проиграл). Ровно столько сыграла Алиса. Заключаем, что она начала во второй игре и проиграла все матчи. Значит, проиграла и во второй партии.
ответ: Алиса
Доказать конгруэнтность этих треугольников можно по признаку УСУ (угол, сторона, угол). Вот теорема:
Если два угла и сторона между ними одного треугольника равны двум углам и стороне между ними другого треугольника, то эти треугольники конгруэнтны (равны).
1) Нам говорят, что отрезок AD является биссектрисой угла BАC. Это означает, что:
Угол ВАD = Угол DAC.
2) Также нам говорят в условии, что угол ADB равняется углу ADC. Угол АDB = Угол ADC.
3) АD является общей стороной этих двух треугольников.
Значит два угла и сторона между ними одного треугольника равны двум углам и стороне между ними другого треугольника, и согласно этому признаку, мы можем сказать, что эти два треугольника конгруэнтны (равны друг-другу).
∆ADB = ∆ADC.