Решить выполнить действия (сложение, вычитание, умножение и деление) над комплексными числами представив результат в форме z1=4+2i и z2=-3+2i раскрыть скобки используя формулы сокращенного умножения (8+6i)(8-6i) решите уравнения 2x²+10x+17=0

Найдем трехзначное число, кратное 24, сумма цифр которого также равна 24.
Пусть искомое число abc, где а - число сотен, b - число десятков, а с - число единиц.
По условиям задачи a+b+c=24, а также abc:24 без остатка.
24 можно представить как сумму трех чисел:
9+8+7
9+7+8
7+9+8
7+8+9
8+9+7
8+7+9
6+9+9
9+9+6
9+6+9
8+8+8
Число 24 можно представить как произведение чисел 3, 4 и 2, значит искомое трехзначное число должно быть кратным 2 (заканчиваться на 0 или четное число), 4 (последние две цифры должны делиться на 4) и 3 (сумма цифр числа кратна 3).
Трем кратны все числа (т.к.сумма 24:3=6), а двум:

9+7+8
7+9+8
9+9+6
8+8+8

Четырем кратны: 9+9+6=8+8+8 (96:4=24; 88:4=22)
Проверим на кратность 24:
996:24=41,5
888:24=37
ответ: 888

область определения это все допустимы значения х

a)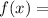

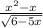
дана дробь, в которой знаменатель имеет переменную х ,а также в знаменателе имеется корень⇒ знаменатель не может быть отрицательным ( так как вычленять из под корня отрицательные значения нельзя) и не может быть равен нулем(делить на ноль нельзя)

получаем  

√(6x-5)>0

6x-5>0

6x>5

x  ∈  (1.2;∞) ⇒ область определения (1.2;∞)

b)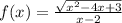

тут тоже самое но √(x²-4x+3)≥0 (так как вычленять из под корня отрицательные значения нельзя)

x-2≠0 (делить на ноль нельзя)

x-2≠2 ⇒x≠2 ⇒  x ∈   (-∞;2) ∪ (2;∞)

√(x²-4x+3)≥0

x²-4x+3≥0

a=1>0 ⇒ интервал знакопостоянства таков

+  корень уравнения   -    корень уравнения    +

x²-4x+3=0

D=(-4)²-4×3×1=4

x=(4±√4)÷2=1  и 3

учитывая интервал и нестрогое неравенство

⇒ x ∈ (-∞;1] ∪ [3;∞)

теперь находим область определения

(  (-∞;1] ∪ [3;∞)  )   ∩    ( (-∞;2) ∪ (2;∞) ) = (-∞;1] ∪ [3;∞)

область определения  (-∞;1] ∪ [3;∞)

c)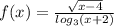

тут уже логарифмы результат логарифмы не должен быть 0 а значит

х+2≠1  ⇒х≠2  ⇒ х ∈ ( -∞;-1) ∪ (-1;∞)

в числителе корень значит

√(х-4)≥0

x-4≥0

x ∈  [4;∞)

ищем область определения

[4;∞)  ∩  ( ( -∞;-1) ∪ (-1;∞) ) = [4;∞)

область определения   [4;∞)