Пусть AL - медиана, а ВК - биссектриса, а т.Н - их точка пересечения.
Рассмотрим треугольник ABL, в нём биссектриса является высотой(пересекаются под прямым углом по условию), следовательно это равнобедренный треугольник. Следовательно, AB=BC=LC. По основному сво-ву биссектрисы треугольника составим следующую пропорцию: AK/KC=AB/BC, следовательно 2*AK=КС, а АС= 3*КС. (т.к. АВ=2*ВС - по условию). Отсюда АН=НL=164/2=82(т.к. в равнобедренном треугольнике высота=бис=медиане)
После, проведём через вершину В прямую, параллельную АС. Она пересечётся с продолжением АL. Пусть точка пересечения будет Д. Отсюда имеем ВД=АС.
Рассмотрим треугольники АHK и BHД. Они подобны ( по трём углам, угол BHД=AHK=90, а угол HAK= углу BДH(как накрест лежащие)).
Распишем отношения сторон: КН/ВН=АК/ВД=1/3. Следовательно НК=164*1/3=164/3 (это примерно 54,666)
Пусть O точка пересечений биссектрисы BE и медианы AD. По условию BE⊥AD, откуда следует что BO биссектриса и высота, следовательно, треугольник ABD равнобедренный: AB=BD и BO медиана. Отсюда
AO=OD=AD/2=16/2=8.
Проведём DF так, чтобы DF║BE. Так как AD медиана, то BD=DC, следовательно DF средняя линия в треугольнике BEC. Отсюда, по свойству средней линии
DF=BE/2=16/2=8.
По построению OE║FD. Так как BO медиана, то AO=OD, следовательно OE средняя линия в треугольнике ADF. Отсюда, по свойству средней линии
OE=DF/2=8/2=4.
По условию BE⊥AD, что и OE⊥AD. Тогда треугольник AOE прямоугольный с гипотенузой AE. Применим теорему Пифагора:
AE²=AO²+OE²=8²+4²=64+16=80=4²·5,
откуда
По условию BE - биссектриса и по свойству биссектрисы
Как отметили ранее, AB=BD=BC/2 и BD=DC, то есть BC=2·AB. Поэтому
Теперь можем найти
(ед.).
Используя OE=4 находим
BO=BE-OE=16-4=12.
Так как BE⊥AD, то треугольник AOB прямоугольный с гипотенузой AB. Применим теорему Пифагора:
АВ=136,6 ВС=273,2 АС=246.99
Пошаговое объяснение:
Пусть AL - медиана, а ВК - биссектриса, а т.Н - их точка пересечения.
Рассмотрим треугольник ABL, в нём биссектриса является высотой(пересекаются под прямым углом по условию), следовательно это равнобедренный треугольник. Следовательно, AB=BC=LC. По основному сво-ву биссектрисы треугольника составим следующую пропорцию: AK/KC=AB/BC, следовательно 2*AK=КС, а АС= 3*КС. (т.к. АВ=2*ВС - по условию). Отсюда АН=НL=164/2=82(т.к. в равнобедренном треугольнике высота=бис=медиане)
После, проведём через вершину В прямую, параллельную АС. Она пересечётся с продолжением АL. Пусть точка пересечения будет Д. Отсюда имеем ВД=АС.
Рассмотрим треугольники АHK и BHД. Они подобны ( по трём углам, угол BHД=AHK=90, а угол HAK= углу BДH(как накрест лежащие)).
Распишем отношения сторон: КН/ВН=АК/ВД=1/3. Следовательно НК=164*1/3=164/3 (это примерно 54,666)
Следовательно ВН=164*2/3=328/3 (это примерно 109,333). Отсюда АВ^2=ВН^2+АН^2, следовательно АВ=136,6, отсюда ВС=2*136,6=273,2
АК^2=HK^2+AH^2, отсюда AК= 82.33. АС=3*82.33=246.99.
(но на ОГЭ советую считать с корнями и не округлять, как это делал я)
Пошаговое объяснение:
Дано (см. рисунок):
ΔABC
BE - биссектриса
AD - медиана
BE⊥AD
BE=AD=16 (ед.)
Найти AB, BC, CA.
Решение.
Пусть O точка пересечений биссектрисы BE и медианы AD. По условию BE⊥AD, откуда следует что BO биссектриса и высота, следовательно, треугольник ABD равнобедренный: AB=BD и BO медиана. Отсюда
AO=OD=AD/2=16/2=8.
Проведём DF так, чтобы DF║BE. Так как AD медиана, то BD=DC, следовательно DF средняя линия в треугольнике BEC. Отсюда, по свойству средней линии
DF=BE/2=16/2=8.
По построению OE║FD. Так как BO медиана, то AO=OD, следовательно OE средняя линия в треугольнике ADF. Отсюда, по свойству средней линии
OE=DF/2=8/2=4.
По условию BE⊥AD, что и OE⊥AD. Тогда треугольник AOE прямоугольный с гипотенузой AE. Применим теорему Пифагора:
AE²=AO²+OE²=8²+4²=64+16=80=4²·5,
откуда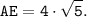
По условию BE - биссектриса и по свойству биссектрисы
Как отметили ранее, AB=BD=BC/2 и BD=DC, то есть BC=2·AB. Поэтому
Теперь можем найти
Используя OE=4 находим
BO=BE-OE=16-4=12.
Так как BE⊥AD, то треугольник AOB прямоугольный с гипотенузой AB. Применим теорему Пифагора:
AB²=AO²+OB²=8²+12²=64+144=208=4²·13,
откуда
Из AB=BC/2 находим: