решить задачу.
Катя одна может собрать со всех кустов ягоды за 4 часа. Когда она отработала 20 минут , ей Маша и они обе собрали все ягодыюОказалось , что они набрали одинаковое количество ягод. За сколько Маша одна собрала бы ягоды со всех кустов?

Это известная задача. Делим слитки на три кучки по три слитка. Кладем первую кучку в одну чашу, вторую - во вторую. Если вес окажется одинаковый, фальшивый слиток лежит в третьей кучке. Если вес окажется разный, фальшивый слиток лежит  в более легкой кучке. Таким образом, одно взвешивание свело задачу с 9 слитками к задаче с 3 слитками. Положив один из них в одну чашу, о второй в другую чашу, поймем, какой слиток фальшивый (если весы будут в равновесии, фальшивым будет третий слиток, если нет, видим, какой слиток легче и тем самым является фальшивым).    

Пошаговое объяснение:

Нам нужно выразить число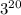 в виде степени с основанием 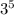. Для этого стоит вспомнить что при возведении степени в степень, основание (или число) степени остаётся без изменения, а показатели степеней перемножаются. То есть наглядно это выглядит так: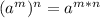

То есть нам нужно разложить 20 степень так, чтобы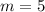 . К счастью это не составит проблем, так как 20 без проблем делится на 5, чтобы найти второе число, после которого наше число можно записать как число со степенью в степени. Поэтому если 20 поделить на 5, то мы получим 4. То есть исходя из формулы выше 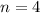, а значит все число имеет вид:

.