(см. объяснение)
Пошаговое объяснение:
Даны две параллельные прямые:
Рассмотрим, например, второе уравнение прямой:
Тогда понятно, что уравнение перпендикулярной ей прямой имеет вид:
, где m - произвольное число.
Для удобства вычислений примем, что .
Тогда:
Не сложно понять, что эта прямая проходит через точку .
Также и первая прямая содержит эту точку.
(это сразу видно из уравнений прямых).
Тогда точка пересечения этих прямых имеет координату .
Решим систему уравнений:
Откуда координата точки будет .
Тогда искомое расстояние равно:
Замечу, что при решении можно было воспользоваться готовой формулой.
Уравнение прямой, которая находится на одинаковом расстоянии от данных прямых имеет вид:
Задание выполнено!
20 | 2 48 | 2 98 | 2 36 | 2
10 | 2 24 | 2 49 | 7 18 | 2
5 | 5 12 | 2 7 | 7 9 | 3
1 6 | 2 1 3 | 3
20 = 2² · 5 3 | 3 98 = 2 · 7² 1
1 36 = 2² · 3²
48 = 2⁴ · 3
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
72 | 2 252 | 2
36 | 2 126 | 2
18 | 2 63 | 3
9 | 3 21 | 3
3 | 3 7 | 7
1 1
72 = 2³ · 3² 252 = 2² · 3² · 7
НОД (20; 48) = 2² = 4 НОД (20; 72) = 2² = 4
НОД (48; 98) = 2 НОД (48; 252) = 2² · 3 = 12
НОД (20; 98) = 2 НОД (20; 252) = 2² = 4
НОД (48; 36) = 2² · 3 = 12 НОД (98; 36) = 2
НОД (20; 36) = 2² = 4 НОД (36; 72) = 2² · 3² = 36
НОД (48; 72) = 2³ · 3 = 24 НОД (98; 72) = 2
НОД (36; 252) = 2² · 3² = 36
НОД (98; 252) = 2
НОД (72; 252) = 2² · 3² = 36
НОД (20; 48; 98) = 2
НОД (48; 36; 72) = 2² · 3 = 12
НОД (36; 72; 252) = 2² · 3² = 36
(см. объяснение)
Пошаговое объяснение:
Даны две параллельные прямые:
Рассмотрим, например, второе уравнение прямой:
Тогда понятно, что уравнение перпендикулярной ей прямой имеет вид:
Для удобства вычислений примем, что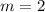 .
.
Тогда:
Не сложно понять, что эта прямая проходит через точку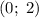 .
.
Также и первая прямая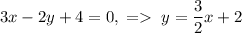 содержит эту точку.
содержит эту точку.
(это сразу видно из уравнений прямых).
Тогда точка пересечения этих прямых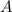 имеет координату
имеет координату 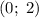 .
.
Решим систему уравнений:
Откуда координата точки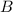 будет
будет 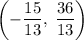 .
.
Тогда искомое расстояние равно:
Замечу, что при решении можно было воспользоваться готовой формулой.
Уравнение прямой, которая находится на одинаковом расстоянии от данных прямых имеет вид:
Задание выполнено!
20 | 2 48 | 2 98 | 2 36 | 2
10 | 2 24 | 2 49 | 7 18 | 2
5 | 5 12 | 2 7 | 7 9 | 3
1 6 | 2 1 3 | 3
20 = 2² · 5 3 | 3 98 = 2 · 7² 1
1 36 = 2² · 3²
48 = 2⁴ · 3
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
72 | 2 252 | 2
36 | 2 126 | 2
18 | 2 63 | 3
9 | 3 21 | 3
3 | 3 7 | 7
1 1
72 = 2³ · 3² 252 = 2² · 3² · 7
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
НОД (20; 48) = 2² = 4 НОД (20; 72) = 2² = 4
НОД (48; 98) = 2 НОД (48; 252) = 2² · 3 = 12
НОД (20; 98) = 2 НОД (20; 252) = 2² = 4
НОД (48; 36) = 2² · 3 = 12 НОД (98; 36) = 2
НОД (20; 36) = 2² = 4 НОД (36; 72) = 2² · 3² = 36
НОД (48; 72) = 2³ · 3 = 24 НОД (98; 72) = 2
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
НОД (36; 252) = 2² · 3² = 36
НОД (98; 252) = 2
НОД (72; 252) = 2² · 3² = 36
НОД (20; 48; 98) = 2
НОД (48; 36; 72) = 2² · 3 = 12
НОД (36; 72; 252) = 2² · 3² = 36