Рассмотрим функцию , ее можно переписать следующим образом: . Переформулируем задачу: найти все значения параметра , при каждом из которых максимальное значение функции не превосходит 5, а минимальное не меньше -5.
Заметим, что . Теперь максимальное и минимальное значения легко определить: , аналогично минимальное: . Значит, и , окончательно:
Рассмотрим функцию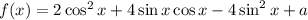 , ее можно переписать следующим образом:
, ее можно переписать следующим образом: 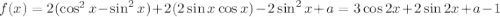 . Переформулируем задачу: найти все значения параметра
. Переформулируем задачу: найти все значения параметра  , при каждом из которых максимальное значение функции
, при каждом из которых максимальное значение функции 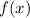 не превосходит 5, а минимальное не меньше -5.
не превосходит 5, а минимальное не меньше -5.
Заметим, что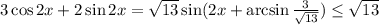 . Теперь максимальное и минимальное значения легко определить:
. Теперь максимальное и минимальное значения легко определить: 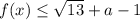 , аналогично минимальное:
, аналогично минимальное: 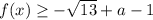 . Значит,
. Значит, 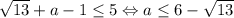 и
и 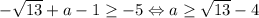 , окончательно:
, окончательно: ![a\in[\sqrt{13}-4,\; 6-\sqrt{13}]](/tpl/images/1358/2025/6a8dd.png)