решить задание Три сотрудника могут составить один и тот же документ. Вероятность представить готовый документ без ошибок для них соответственно равны p1,p2,p3 . Составить закон распределения случайной величины X – числа готовых документов без ошибок, найти её математическое ожидание, дисперсию и среднее квадратическое отклонение.
p1-0.4,
p2-0.9,
p3-0.5,
Пошаговое объяснение:
30% = 30 : 1 00 = 0,3
20% = 20 : 1 00 = 0,2
50% = 50 : 1 00 = 0,5
Купили всего = х компьютеров
Село А = 0,3х компьютера
Село Б = 0,2 * (х - 0,3х) = 0,2 * 0,7х = 0,14х компьютеров
Село А + Село Б = 0,3х + 0,14х = 0,44х
Село С = 0,5 * (х - 0,44х) = 0,5 * 0,56х = 0,28х компьютеров
Село Д = 14 компьютеров
0,3х + 0,14х + 0,28х + 14 = х
0,72х + 14 = х
0,72х - х = -14
-0,28х = -14
х = -14 : (-0,28)
х = 50
Купили всего компьютеров = (х) = 50 штук
Село А = (0,3х) = 0,3 * 50 = 15 компьютеров
Село Б = (0,14х) = 0,14 * 50 = 7 компьютеров
Село С = (0,28х) = 0,28 * 50 = 14 компьютеров
Село Д = 14 компьютеров
15 + 7 + 14 + 14 = 50
∠M=30°, ∠R=30°, ∠Т=120°,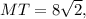
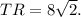
Пошаговое объяснение:
Рассмотрим Δ MTR - равнобедренный.
В равнобедренном треугольнике углы при сновании равны.
Значит,
∠M= ∠R=30°.
Так как сумма углов треугольника равна 180°, то
∠Т= 180°-(30°+30°)=180°-60°=120°
По условию основание
В равнобедренном треугольнике проведем высоту к основанию, она является медианой. Значит,
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Рассмотрим Δ MNT - прямоугольный.
Так как треугольник равнобедренный, то