Несмотря на то, что стрижи и ласточки очень похожи внешне, они даже не родственники: ласточки относятся к отряду воробьиных, а стрижи - к отряду стрижеобразных (или длиннокрылых). Кроме того, ласточка как летун в подметки не годится стрижу! Стриж - чемпион среди всех птиц по скорости полета (120-160 км/ч), ласточка же летает гораздо медленнее - со скоростью 50-60 км/ч. Стриж летает стремительно и по прямой, но проигрывает ласточке по маневренности полета.Характерных внешних отличий у стрижей и ласточек достаточно много.У стрижей и ласточек различается строение лапки. У ласточки, как у любой другой птицы, три пальца направлены вперед и один - назад. У стрижа же все четыре пальца на лапке направлены вперед. Такой лапкой не удержишься на ветке, но зато ею, как альпинистскими крючками, можно зацепиться за малейший выступ или щелочку на вертикальной поверхности, деревянной или каменной. Поэтому, если вы видите семейку птиц с раздвоенным хвостиком, сидящую на телеграфных проводах, можете не сомневаться, что это не стрижи, а ласточки.Однако, чтобы разглядеть лапку птички, к ней нужно подобраться совсем близко или даже поймать ее. Как же различить стрижа и ласточку в полете?У ласточек грудка белая, а у стрижей только белое пятнышко под клювом. Поэтому у летающего стрижа вы хорошо можете разглядеть темное брюшко, а у ласточки - белое.Стриж, в отличие от ласточки, в полете никогда не складывает крылья.Стрижи отличаются от ласточек крикливостью. В полете они постоянно и громко визжат.Стриж крупнее ласточки, его крылья уже, но значительно длиннее и имеют серповидную форму. Хвост стрижа более широкий и более короткий.
; Поэтому у данной функции есть период. Просмотрим остальные:
; Пусть у этой функции есть период T: ; Выберем такое число x и n, что выполняются следующие условия: ; Тогда левая часть будет больше правой, что невозможно.
; Пусть функция имеет период T:
; Получили противоречие.
С оставшимися аналогично.
ответ: А;
2) ; Функция монотонно убывает по мере роста показателя степени.
Заметим, что ; Значит, ;
3) ; С этими условиями область значений равна [-2;2]; Если брать в расчет все значения x, то придется выколоть все точки с ординатами 2 или -2; Получаем, что E(f)=(-2;2);
4) Пусть sin A - первый корень какого-нибудь квадратного трехчлена, а -cos A - его второй корень. Тогда квадратное уравнение примет такой один из возможных видов: ;
1)
С оставшимися аналогично.
ответ: А;
2)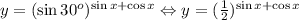 ; Функция монотонно убывает по мере роста показателя степени.
; Функция монотонно убывает по мере роста показателя степени.
Заметим, что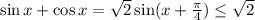 ; Значит,
; Значит, 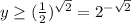 ;
;
3)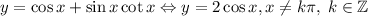 ; С этими условиями область значений равна [-2;2]; Если брать в расчет все значения x, то придется выколоть все точки с ординатами 2 или -2; Получаем, что E(f)=(-2;2);
; С этими условиями область значений равна [-2;2]; Если брать в расчет все значения x, то придется выколоть все точки с ординатами 2 или -2; Получаем, что E(f)=(-2;2);
4) Пусть sin A - первый корень какого-нибудь квадратного трехчлена, а -cos A - его второй корень. Тогда квадратное уравнение примет такой один из возможных видов: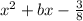 ;
;
В итоге, получаем: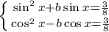 ; Сложим два уравнения:
; Сложим два уравнения: