Решите как можно подробней log0,4(x²-6x-10)=log0,4(10-8x)

Плоскость треугольника АВС пересекает параллельные плоскости α и β по параллельным прямым.
ВС║В₁С₁║В₂С₂

По условию AB₁ = B₁B₂ = B₂B = 8/3 см, тогда по теореме Фалеса
AС₁ = С₁С₂ = С₂С = 8/3 см

ΔАВС подобен ΔАВ₁С₁ по двум углам (∠АВ₁С₁ = ∠АВС и ∠АС₁В₁ = ∠АСВ как накрест лежащие)

В₁С₁ : ВС = АВ₁ : АВ = 1 : 3
В₁С₁ = 8/3 см

ΔАВС подобен ΔАВ₂С₂ по двум углам (∠АВ₂С₂ = ∠АВС и ∠АС₂В₂ = ∠АСВ как накрест лежащие)

В₂С₂ : ВС = АВ₂ : АВ = 2 : 3
В₂С₂ = 2·8/3 = 16/3 см

а) треугольник АВС разбивается на
равносторонний треугольник АВ₁С₁;
трапецию В₂В₁С₁С₂;
трапецию ВВ₂С₂С.
б) Pab₁c₁ = (8/3) · 3 = 8 cм
Pb₂b₁c₁c₂ = 8/3 + 8/3 + 8/3 + 16/3 = 40/3 = 13 и 1/3 см
Pbb₂c₂c = 8/3 + 16/3 + 8/3 + 8 = 56/3 = 18 и 2/3 см

а) ошибки не будут обнаружены;    вероятность = 1/30

б) будет обнаружена хотя бы одна ошибка  вероятность = 29/30

Пошаговое объяснение:

Наше событие

А = {из 6 выбранных отчетов хотя бы одна ошибка }

Противоположное событие

= { из 6 выбранных отчетов ни одной ошибки} =

   = {все 6 отчетов верные} =

   = { ошибки не будут обнаружены }

Запишем вероятность события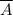 по формуле классического определения вероятности.

Общее число исходов

Благоприятное число исходов (выбрать 6 правильных отчетов из 7 правильных)

Таким образом вероятность того, что все 6 отчетов будут верные, т.е.

а) ошибки не будут обнаружены

б)  будет обнаружена хотя бы одна ошибка

#SPJ1