Пошаговое объяснение:ответы на тест по тригонометрии.
Задание 1. Уравнение вида a sin2x + b sinx cosx + c cos2x = 0 называют однородным тригонометрическим уравнением второй степени.
Алгоритм решения однородного тригонометрического уравнения первой степени:
1.Посмотреть, есть ли в уравнении член asin2 x.
2.Если член asin2 x в уравнении содержится (т.е. а 0), то уравнение решается делением обеих частей уравнения на cos2x и последующим введение новой переменной.
3.Если член asin2 x в уравнении не содержится (т.е. а = 0), то уравнение решается методом разложения на множители: за скобки выносят cosx.
Задание 2. 1 уравнение из перечисленных не являются однородными, Это уравнение: 5 Sinx +3 Cosx =1 ответ:1
Задание 3. ответ:5. 5 уравнений из перечисленных являются однородными, Это уравнения: 1) 5sinx+3Cosx=0, 2) 5Sin2x+3SinxCosx+3Cos2x=0, 3) 5Sin2x+3SinxCosx+3Cos2x=3, 4) 5Sin2x+3SinxCosx = 3Cos2x, 5) Sinx=Cosx
Число различных перестановок из n элементов обозначается Pn и вычисляется по формуле Pn=n!. Используя эту формулу, решается задача 1) и 2) - ответами в обоих будет число 24. Для задачи 3) введем формулу (на картинке), где m - количество элементов в конечной выборке (т.е. то кол-во мужчин, которые садятся на скамейку), а n - кол-во элементов массива(кол-во свободных на скамейке мест). Подставив все величины в формулу, получим :
ответ: ответы в файле
Пошаговое объяснение:ответы на тест по тригонометрии.
Задание 1. Уравнение вида a sin2x + b sinx cosx + c cos2x = 0 называют однородным тригонометрическим уравнением второй степени.
Алгоритм решения однородного тригонометрического уравнения первой степени:
1.Посмотреть, есть ли в уравнении член asin2 x.
2.Если член asin2 x в уравнении содержится (т.е. а 0), то уравнение решается делением обеих частей уравнения на cos2x и последующим введение новой переменной.
3.Если член asin2 x в уравнении не содержится (т.е. а = 0), то уравнение решается методом разложения на множители: за скобки выносят cosx.
Задание 2. 1 уравнение из перечисленных не являются однородными, Это уравнение: 5 Sinx +3 Cosx =1 ответ:1
Задание 3. ответ:5. 5 уравнений из перечисленных являются однородными, Это уравнения: 1) 5sinx+3Cosx=0, 2) 5Sin2x+3SinxCosx+3Cos2x=0, 3) 5Sin2x+3SinxCosx+3Cos2x=3, 4) 5Sin2x+3SinxCosx = 3Cos2x, 5) Sinx=Cosx
Задание 4. ответ: 1)сCos2x , 2)aSin2x , 4)bSinxCosx
Задание 5. ответ: варианты 1 и 3.
Задание 6. ответ: 4) Задание 7. ответ: 2) и 5)
Задание 8. ответ: 2) и 3)
Задание 9. ответ: вариант 4)
Задание 10. ответ: 2(два уравнения однородные 1 степени)
Пошаговое объяснение:
Число различных перестановок из n элементов обозначается Pn и вычисляется по формуле Pn=n!. Используя эту формулу, решается задача 1) и 2) - ответами в обоих будет число 24. Для задачи 3) введем формулу (на картинке), где m - количество элементов в конечной выборке (т.е. то кол-во мужчин, которые садятся на скамейку), а n - кол-во элементов массива(кол-во свободных на скамейке мест). Подставив все величины в формулу, получим :
C =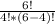
= 15 возможностей их различной посадки