Решите надо математика 6 класс.
Решите 4и5и6.
Заранее благодарен

Показать ответ

Ответ:

CassyBelka

16.04.2020 03:44

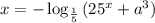
7. $x=-\log_{\frac{1}{5}}{(25^x+a^3)}$

$x=\log_5{(25^x+a^3)}\\5^x=25^x+a^3\\5^x-25^x=a^3$

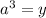Пусть a^3=y , количество корней от этого не изменится.

Рассмотрим функцию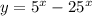 y=5^x-25^x :

$\lim_{x \to -\infty}{y}=0\\ \lim_{x \to \infty}{y}=-\infty\\y'=\ln{5}*5^x-2\ln{5}*25^x\\\ln{5}*5^x-2\ln{5}*25^x=0\\5^x=2*25^x\\\frac{1}{2}=5^x\Leftrightarrow x=-\log_5{2}$

До точки экстремума функция возрастает, а после — убывает. Значит, это точка максимума. Максимальное значение функции равно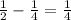 $\frac{1}{2}-\frac{1}{4}=\frac{1}{4}$ . Прикинем график функции (см. рис. 1). Уравнение имеет 2 различных решения, если:

ответ: $(0; \frac{\sqrt[3]{2}}{2})$

8. При изменении размеров пирамиды соотношения между соответственными элементами не изменятся, поэтому примем для простоты вычислений сторону основания за 1.

Рассмотрим первую пирамиду:

Пусть SKM — сечение пирамиды SABCD, где K и M — середины BC и AD соответственно. Тогда в это сечение попадает окружность, вписанная в треугольник SKM и касающаяся KM в точке S' (проекция точки S), SK в точке K'. Пусть ∠SKS' = α, KO₁ — биссектриса, тогда:

$\alpha=arctg \frac{SS'}{S'K}=arctg\ 4\sqrt{3}\\R_1=O_1S'=S'Ktg\frac{\alpha}{2}$

$tg\alpha=\frac{2tg\frac{\alpha}{2}}{1-tg^2\frac{\alpha}{2}}\\tg\frac{\alpha}{2} =x\\4\sqrt{3}=\frac{2x}{1-x^2}\\4\sqrt{3}-4\sqrt{3}x^2=2x\\4\sqrt{3}x^2+2x-4\sqrt{3}=0\\t^2+2t-48=0\Rightarrow t_1=-8, t_2=6 \Rightarrow x_1=-\frac{2}{\sqrt{3}}, x_2=\frac{\sqrt{3}}{2}$

Учитывая, что угол находится в первой четверти,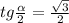 $tg\frac{\alpha}{2}=\frac{\sqrt{3}}{2}$

$R_1=\frac{1}{2}*\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{4}$

Рассмотрим вторую пирамиду:

Пусть S₁A₁C₁ — сечение пирамиды S₁A₁B₁C₁D₁. Это сечение содержит окружность, вписанную в треугольник S₁A₁C₁, касающуюся стороны A₁C₁ в точке S₁' (проекция точки S₁) и стороны S₁A₁ в точке A₁'. Пусть ∠S₁A₁S₁' = β, A₁O₂ — биссектриса. Тогда:

$\beta=arctg \frac{S_1S_1'}{A_1S_1'}=arctg\ 2\sqrt{6}\\R_2=O_2S_1'=S_1'A_1tg\frac{\beta}{2}$

Решая аналогичное уравнение, получаем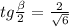 $tg\frac{\beta}{2}=\frac{2}{\sqrt{6}}$

$R_2=\frac{1}{\sqrt{2}}*\frac{2}{\sqrt{6}}=\frac{\sqrt{2}}{\sqrt{6}}=\frac{1}{\sqrt{3}}$

$\frac{R_2}{R_1}=\frac{\frac{1}{\sqrt{3}}}{\frac{\sqrt{3}}{4}}=\frac{4}{3}$

ответ: 4 : 3

0,0(0 оценок)

Ответ:

aitbek99

25.04.2023 07:21

1. 422715:15+918936:36=53707
422715:15=28181
918936:36=25526
28181+25526=53707

2. 51243:3/8=51243*8:3=136648

3. 20-2=18 км\ч-скорость теплохода, идущего против тчения реки
20+2=22 км\ч-скорость теплохода, идущего по течению реки
18+22=40 км\ч-скорость сближения
120:40=3 часа
ответ: встреча произойдет через 3 часа

4.36:6=6м\ч-папа в час красит 6 метров
36:12=3 м/ч-сын красит 3 метра в час
3+6=9 м\ч-вместе в час красят 9 м
36:9=4 часа
ответ: за 4 часа

5.900:5=180 руб-такова должна быть стоимость 1 набора
если возьмем по 1 кг какждого овоща, то стоимость 1 набора будет составлять=30+40+20+15+25=130 руб То есть в каждый набор надо добирать овощей на 50 руб.
Это может быть : 1) огурцы(30 руб)+капуста(20 руб) 2) свекла-2кг(30 руб)+капуста-1кг(20 руб) 3)кабачки-2 кг(50 руб)
ответ: возможные наборы: 1) огурцы-2 кг, помидоры-1 кг, капста-2 кг, свекла-1 кг, кабачки-1кг 2)огурцы-1кг, помидоры-1 кг, капуста-2 кг, свекла-3 кг,кбачки-1 кг 3)огурцы-1 кг, помидоры-1 кг, капуста-1 кг, свекла-1 кг, кабачки-3 кг

0,0(0 оценок)

Популярные вопросы: Математика