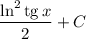Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
Юлия250501
31.08.2020 06:34 •
Математика
Решите неопределенный интеграл
Показать ответ
Ответ:
BlackCat20101
12.10.2020 01:22
Как нашли
ответ:
0,0
(0 оценок)
Популярные вопросы: Математика
НастяБлог
17.10.2020 15:15
Приведи дроби 4a/b2, 5a-b/a+b и 7/bк общему знаменателю....
asikpozitiv3
19.05.2020 23:14
Вычислить lim x- 0 ((1+tgx)/(1+sinx))^(1/sinx) через формулу lim f (x)^g(x)=e^lim g(x) ln f(x)...
Marg06
02.03.2022 08:22
Начерти втетради 3одинаковых прямоугольника,длины сторон каждого из которых 3см и4см. Проведи в каждом из них один отрезок так, чтобы он разделил первый прямоугольник на...
dashasviridenko
17.03.2023 03:51
В лаборатории есть 6 автоматов и 4 полуавтомата. Вероятность того, что за час выполнения работы автомат не откажет, равна 0,95, для полуавтомата - 0,8. При выполнении работы...
GoldenLynx1999
09.01.2022 05:19
3 9 12 және 12бөлшектерінің арасында орналасқан, бөлімі 12-ге тең жай бөлшектерді өсу ретімен жаз....
leralerochka202
31.01.2022 07:19
РЕШИТЬ МАТРИЧНОЕ УРАВНЕНИЕ РЕШЕНИЕ РАСПИШИТЕ...
zamanova05
26.07.2022 15:17
C*8-9344=24520 5689+7*a=23665 быстрее ал...
Maksikikl
26.07.2022 15:17
3. Придумайте задачу по выражению:а) 120 + 65 - 2; б) 168 — 43 : 2;...
Katylopy
25.02.2020 16:47
Определить верное неравенство 2*2*2*2=2*4...
San4ic
03.10.2021 11:26
Боялған бөлікті көрсететін аралас санды анықта....
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Как нашли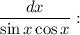
ответ: