Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
feitlol
13.04.2022 23:04 •
Математика
Решите неравенство 5^(х+2) + 5^(х+1) - 5^х < 3^(0,5х +1) - 3^0,5х - 3^(0,5х-1)
Показать ответ
Ответ:
amina347
09.10.2020 06:08
Перенесём всё в одну часть.
Поделим обе части на
Прологарифмируем по основанию
и получим
0,0
(0 оценок)
Популярные вопросы: Математика
polinaguskova
10.04.2021 19:13
Математика 779есеп5классКөмек ...
думайй
12.05.2022 22:18
3) [2; +бес.) и (7; +бес.) о ооо ...
lkivaka
26.04.2023 09:58
1236*4 708*8 3600*5 2448:3 7528:2 8910:9...
OLZHAS1808
24.01.2022 03:07
В саду высадили 80 елей,что составило 40 % всех деревьев.Сколько всего деревьев?...
dbrnjhbzybr
30.03.2023 19:48
А) в тоннах: 245 ц; 5-7 кг; 7 т 2 ц 65 кг;б) в квадратных дециметрах:8 дм2 63 см; 37 дм? 8 см2;11 м2 4 см2....
рпипппит
26.03.2020 11:58
Здравствуйте Найдите произведение, если первый множитель 1,7 а второй 2,3? 2)Лодка движется по реке со скоростью 5,3км/ч какое расстояние она пройдёт за 0,2 ч? 3)найдите...
fyjdtjjhtjh
16.05.2021 14:32
Купили ковбасу , сир , масло , разом 900г Масса ковбаси і сиру 700г, мор і масло 470г Яка маса кожного продукту ?...
fffg16hgkk
02.06.2020 23:35
решить задачу. У торговца Махлюшкина имеется на продажу 360 кг овощей.4/9 овощей составляет картофель.7/24-морковь, а остальное -лук.Сколько килограммов лука у торговца...
лунный3
25.03.2023 00:21
Один рабочий изготовил за день 23 детали , а другой -21 делать. Сколько деталей изготовлена за 2 дня...
Pots150204
25.12.2022 19:13
Решите неравенство и изобразите множество его решений на координатной прямой: 1) 4х-3 ≥02) -5х...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Перенесём всё в одну часть.
Поделим обе части на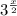
Прологарифмируем по основанию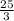 и получим
и получим