Проверять дальнейшие "наборы" натуральных чисел не требуется, так как сумма слева всегда будет больше суммы справа. Докажем это. Пусть n - наименьшее натуральное число, причём n>5. Тогда сумма слева S1=n+n+1+n+2=3*n+3, а сумма справа S2=n+3+n+4=2*n+7. Рассмотрим разность S1-S2=n-4. Очевидно, что при n>4 эта разность всегда положительна.
5. Пусть v1 - скорость катера, v2 - скорость течения, t - время. Тогда (v1+v2)*t+(v-v2)*t=2*v1*t=90+70=160 км, а v1*t=160/2=80 км.
ответ: 4) 4,5,6,7,8 5) 80 км.
Пошаговое объяснение:
4.
1) 1+2+3<4+5;
2) 2+3+4<5+6;
3) 3+4+5<6+7;
4) 4+5+6=7+8;
5) 5+6+7>8+9
Проверять дальнейшие "наборы" натуральных чисел не требуется, так как сумма слева всегда будет больше суммы справа. Докажем это. Пусть n - наименьшее натуральное число, причём n>5. Тогда сумма слева S1=n+n+1+n+2=3*n+3, а сумма справа S2=n+3+n+4=2*n+7. Рассмотрим разность S1-S2=n-4. Очевидно, что при n>4 эта разность всегда положительна.
5. Пусть v1 - скорость катера, v2 - скорость течения, t - время. Тогда (v1+v2)*t+(v-v2)*t=2*v1*t=90+70=160 км, а v1*t=160/2=80 км.
1.22 Длина = k + i, периметр = 2·(ширина + длина) = 2(i+k+i) = 2(2i+k)
ответ: периметр равен 2(2i+k) дециметров
1.23 ответ: сторона равна g : 3 = дм
дм
1.24 Длина = k см, ширина = h дм = 10h см (1 дм = 10 см) ⇒ периметр равен 2·(k + 10h) = 2(10h + k) сантиметров.
ответ: периметр равен 2(10h + k) см
1.25 Пусть L - длина проволоки. Периметр участка равен 2(q+d+q) =
2(2q + d), тогда L = 2(2q + d)*k = 2k(2q + d);
ответ: потребовалось 2k(2q + d) метров проволоки
1.26 Площадь одной плитки = i² дм², требуется облицевать площадь
d*k дм² ⇒ N - искомое число плиток равно (d*k) : i² =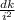
ответ: