Чтобы было нагляднее, вычтем из всех частей этого неравенства :
Выражение не может быть одновременно и больше, и меньше нуля (это одна из аксиом алгебры: для любых двух чисел и выполняется одно и только одно из соотношений: ), поэтому оно может равняться только нулю:
В мат. анализе с приведения к подобному неравенству (только для функций) доказывается существование первого замечательного предела - "теорема о двух конвоирах (миллиционерах)"
Решение простое. х ≥ а², когда х либо больше, либо равно а².
Другая часть неравенства х ≤ а², когда х либо меньше, либо равно а².
Пересечение решений, т.е. их общее решение х=а² и будет ответом. а²≤а²≤а², т.е. при х=а² выполняется как одна часть неравенства, так и другая, поэтому х=а²
Чтобы было нагляднее, вычтем из всех частей этого неравенства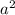 :
:
Выражение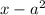 не может быть одновременно и больше, и меньше нуля (это одна из аксиом алгебры: для любых двух чисел
не может быть одновременно и больше, и меньше нуля (это одна из аксиом алгебры: для любых двух чисел  и
и 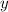 выполняется одно и только одно из соотношений:
выполняется одно и только одно из соотношений: 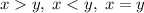 ), поэтому оно может равняться только нулю:
), поэтому оно может равняться только нулю:
В мат. анализе с приведения к подобному неравенству (только для функций) доказывается существование первого замечательного предела - "теорема о двух конвоирах (миллиционерах)"
Решение простое. х ≥ а², когда х либо больше, либо равно а².
Другая часть неравенства х ≤ а², когда х либо меньше, либо равно а².
Пересечение решений, т.е. их общее решение х=а² и будет ответом. а²≤а²≤а², т.е. при х=а² выполняется как одна часть неравенства, так и другая, поэтому х=а²
ответ х=а²